質數的歷史與應用
Prime Numbers: From Ancient Greece to Modern Cryptography
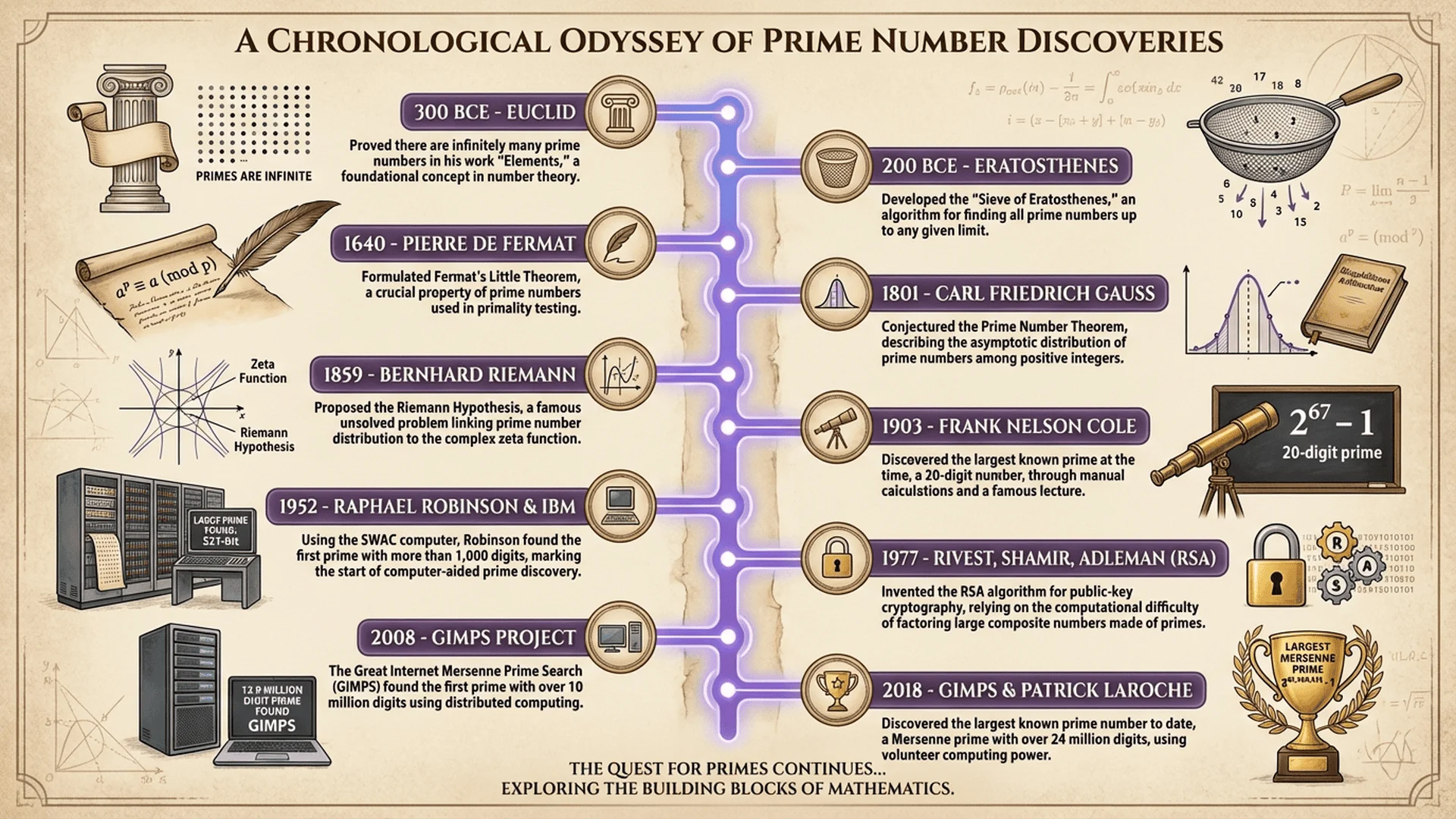
Introduction: 2,300 Years of Mathematical Obsession
Prime numbers—integers divisible only by 1 and themselves—are among humanity's oldest mathematical discoveries, yet they remain at the cutting edge of modern technology. The same concept that fascinated Euclid in 300 BCE now secures your online banking, encrypts your messages, and protects state secrets in 2025.
Why have primes captivated mathematicians for millennia? Unlike most mathematical patterns, prime numbers appear random yet fundamental—they're the "atoms" of arithmetic, the building blocks from which all other numbers are constructed through multiplication. Yet despite 2,300 years of study, fundamental questions remain unanswered: Is there a formula to generate all primes? Why do they follow certain statistical patterns? Will quantum computers change everything?
This journey through prime number history reveals three revolutionary eras:
- Ancient foundations (300 BCE - 1600 CE): Euclid's infinitude proof, Eratosthenes' sieve, and centuries of hand calculation
- Computational explosion (1600 - 1970): Mersenne primes, Fermat's Little Theorem, and the first computers tackling primality
- Cryptographic revolution (1977 - present): RSA encryption transforms primes from mathematical curiosity to trillion-dollar infrastructure
Today, every time you see "https://" in your browser, buy something on Amazon, or send a WhatsApp message, prime numbers are working invisibly to protect you. Let's explore how ancient Greek geometry evolved into the backbone of digital civilization.
Want to understand the technical side? Check our Prime Number Check Complete Guide for modern algorithms, or explore our Prime Algorithms Comparison to see how historical methods evolved into today's techniques.
Image Description:
-
Scene Description: A recreation of an ancient Greek classroom scene (circa 300 BCE), featuring an elderly Euclid (65-70 years old, white beard, wearing a cream-colored Greek chiton/toga, laurel wreath) standing beside a marble column in a sunlit open-air courtyard (peristyle). He's gesturing toward a large papyrus scroll (2 meters long, beige/tan color) mounted on a wooden frame. The scroll displays handwritten Greek numerals and geometric diagrams illustrating prime numbers: a list showing 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31... with some crossed out (demonstrating the Sieve of Eratosthenes concept). Three young students (18-25 years old, wearing simple white tunics) sit on stone benches taking notes on wax tablets. Warm Mediterranean sunlight streams through Ionic columns, casting dramatic shadows. The Parthenon is faintly visible in the background through the columns.
-
Visual Focus: The papyrus scroll with the prime number sequence and the Sieve pattern clearly visible. Euclid's pointing gesture draws attention to the numbers. The handwritten Greek numerals (α, β, γ, δ, ε... for 1, 2, 3, 4, 5...) should be legible and authentic-looking.
-
Must-Appear Elements:
- Elderly Euclid (white beard, laurel wreath, cream toga)
- Large papyrus scroll on wooden frame (2m × 0.5m)
- Greek numerals visible: Β, Γ, Ε, Ζ, ΙΑ, ΙΓ, ΙΖ, ΙΘ... (2, 3, 5, 7, 11, 13, 17, 19...)
- Some numbers crossed out (showing sieve pattern)
- Three students sitting on stone benches with wax tablets
- Ionic marble columns (white with vertical fluting)
- Mediterranean sunlight (warm, golden hour quality)
- Parthenon visible in background (distant, slightly hazy)
-
Stone courtyard floor (light limestone)
-
Chinese Text to Display: None
-
Image/Character Style: Historically accurate recreation, photorealistic rendering, classical Greek aesthetic, warm natural lighting (golden hour, 5000K), shallow depth of field (f/4.0) with focus on scroll and Euclid, cinematic composition, educational documentary style
-
Color Palette:
- Primary: Warm white/cream (#F5E6D3 - toga, columns)
- Secondary: Aged papyrus (#E8D4B0 - scroll)
- Accent: Rich brown (#8B4513 - ink on scroll)
- Supporting: Mediterranean blue (#4A90E2 - distant sky)
-
Highlights: Golden sunlight (#FFD700 - sun rays through columns)
-
Avoid Elements: Modern anachronisms (glasses, books, pens), stock photo clichés, abstract graphics (floating numbers, holograms), overly dramatic "epic" movie lighting, Arabic numerals (should be Greek), circuit boards, computer imagery, arrows, checkmarks as decorations
-
Slug: euclid-prime-numbers-teaching
Part 1 - Ancient Foundations: Euclid to Eratosthenes (300 BCE - 200 CE)
Euclid's Infinitude Proof (300 BCE): The First Bombshell
The discovery: There are infinitely many prime numbers.
Before Euclid, mathematicians knew primes existed—2, 3, 5, 7, 11, 13... were easy to find by hand. But did the sequence end? Was there a "largest prime"? In Euclid's Elements (Book IX, Proposition 20), he proved the answer was a resounding no.
Euclid's elegant proof (paraphrased in modern language):
- Assume there are only finitely many primes: p₁, p₂, p₃, ..., pₙ
- Multiply them all together: N = p₁ × p₂ × p₃ × ... × pₙ
- Add 1: M = N + 1
- Now, M is either prime or composite:
- If M is prime → we found a new prime not in our list! Contradiction.
- If M is composite → it must have a prime factor. But M ÷ p₁ leaves remainder 1, M ÷ p₂ leaves remainder 1, etc. So its prime factor can't be any of p₁...pₙ. Contradiction.
- Therefore, our assumption was wrong—primes are infinite.
Why this matters: Euclid's proof is a masterpiece of proof by contradiction and established that primes are fundamentally inexhaustible. It's still taught in introductory number theory courses 2,300 years later.
Try it yourself:
Known primes: 2, 3, 5
N = 2 × 3 × 5 = 30
M = 30 + 1 = 31 (prime! ✓)
Known primes: 2, 3, 5, 7
N = 2 × 3 × 5 × 7 = 210
M = 210 + 1 = 211 (prime! ✓)
Test any sequence with our free prime checker to see Euclid's logic in action!
Eratosthenes' Sieve (240 BCE): The First Algorithm
The innovation: A systematic method to generate all primes up to any number n.
The Sieve of Eratosthenes was the world's first prime-finding algorithm, remarkable for its simplicity:
- List all numbers from 2 to n
- Start with 2 (smallest prime)
- Cross out all multiples of 2 (4, 6, 8, 10...)
- Move to next uncrossed number (3), cross out its multiples (6, 9, 12, 15...)
- Repeat until reaching √n
- All remaining numbers are prime
Example (finding primes ≤ 30):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Cross multiples of 2:
2 3 ✗ 5 ✗ 7 ✗ 9 ✗ 11 ✗ 13 ✗ 15 ✗ 17 ✗ 19 ✗ 21 ✗ 23 ✗ 25 ✗ 27 ✗ 29 ✗
Cross multiples of 3:
2 3 ✗ 5 ✗ 7 ✗ ✗ ✗ 11 ✗ 13 ✗ ✗ ✗ 17 ✗ 19 ✗ ✗ ✗ 23 ✗ 25 ✗ ✗ ✗ 29 ✗
Cross multiples of 5:
2 3 ✗ 5 ✗ 7 ✗ ✗ ✗ 11 ✗ 13 ✗ ✗ ✗ 17 ✗ 19 ✗ ✗ ✗ 23 ✗ ✗ ✗ ✗ ✗ 29 ✗
Primes ≤ 30: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ✓
Impact: This algorithm is still used today in optimized forms. Modern computers can sieve all primes up to 1 billion in seconds using bit-packing techniques (see our C optimization guide for details).
Historical note: Eratosthenes was also the first person to accurately measure Earth's circumference (within 2% of the true value) using only shadows and geometry. Ancient Greeks were computational powerhouses!
The Dark Ages: 1,500 Years of Slow Progress
200 CE - 1600 CE: Prime number research nearly stalled during the Middle Ages.
Notable developments:
- Fibonacci (1202): Introduced Arabic numerals to Europe in Liber Abaci, making prime calculations easier than Roman numerals
- Pietro Cataldi (1603): Verified that 2^17 - 1 = 131,071 is prime (by hand!)—an early Mersenne prime discovery
Why so slow? Without modern notation or calculating tools, verifying large primes required years of manual arithmetic. Trial division of a 6-digit number could take weeks. Progress awaited better mathematical notation and mechanization.

Part 2 - The Computational Era: From Fermat to Computers (1600 - 1977)
Fermat's Little Theorem (1640): A Primality Test is Born
Pierre de Fermat discovered a property that would become the basis for modern probabilistic primality testing:
Fermat's Little Theorem: If p is prime and a is not divisible by p, then:
a^(p-1) ≡ 1 (mod p)
Example:
Let p = 7 (prime), a = 2
2^(7-1) = 2^6 = 64
64 mod 7 = 1 ✓ (theorem holds)
Let p = 6 (composite), a = 2
2^(6-1) = 2^5 = 32
32 mod 6 = 2 ✗ (theorem fails, confirming 6 is composite)
Why revolutionary: This provided a fast primality test—instead of checking divisors up to √p, just compute a^(p-1) mod p. If it's not 1, p is definitely composite!
The catch: Some composite numbers (Carmichael numbers) fool Fermat's test. This led to modern improvements like Miller-Rabin (see our algorithm comparison).
Mersenne Primes: The Search for Giants (1644 - Present)
Marin Mersenne investigated primes of the form M_p = 2^p - 1 (where p is prime).
Why special?
- Binary simplicity: 2^p - 1 is all 1's in binary (111...111)
- Faster testing: Lucas-Lehmer test is much faster than general primality tests
- Record holders: All largest known primes since 1952 are Mersenne primes
Mersenne's original claim (1644): He stated that M_p is prime for p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257.
Reality check (after 300+ years): Mersenne was wrong about 5 values and missed 3 others! Shows how hard manual verification was.
Current record (2024): M_82,589,933 = 2^82,589,933 - 1 (24,862,048 digits)
- Discovered: December 2018 by GIMPS project
- Would fill ~10,000 book pages if printed
- Took 12 days to verify on a high-end PC
Try finding small Mersenne primes yourself:
def is_mersenne_prime_candidate(p):
# p must be prime first
M_p = (2 ** p) - 1
return M_p
# Test small values
for p in [2, 3, 5, 7, 11, 13]:
M_p = is_mersenne_prime_candidate(p)
print(f"M_{p} = {M_p}")
# Output:
# M_2 = 3 (prime ✓)
# M_3 = 7 (prime ✓)
# M_5 = 31 (prime ✓)
# M_7 = 127 (prime ✓)
# M_11 = 2047 = 23 × 89 (composite ✗)
# M_13 = 8191 (prime ✓)
Verify these with our prime checker or read our large prime detection guide for finding cryptographic-scale Mersenne primes.
The Computer Age: ENIAC to Modern Algorithms (1949 - 1977)
1949: First computer-discovered prime
- ENIAC verifies that 2^127 - 1 is prime in just 2 hours (would take a human ~1 year)
- Ushered in era of computational number theory
1951-1952: Robinson & Lehmer
- Used modified ENIAC to find 5 new Mersenne primes: M_521, M_607, M_1279, M_2203, M_2281
- Each discovery broke the record for "largest known prime"
1964: CDC 6600 supercomputer
- Found M_11,213 (3,376 digits)—largest prime of the 20th century at the time
1970s: Algorithms mature
- Miller-Rabin test (1976): Probabilistic primality testing becomes practical
- AKS algorithm concept forms: Ideas brewing for deterministic polynomial-time test (proven in 2002)
Key realization: Computers didn't just speed up old methods—they enabled entirely new algorithms (like Miller-Rabin) impossible to execute by hand.
Part 3 - The Cryptographic Revolution: RSA and Beyond (1977 - Present)
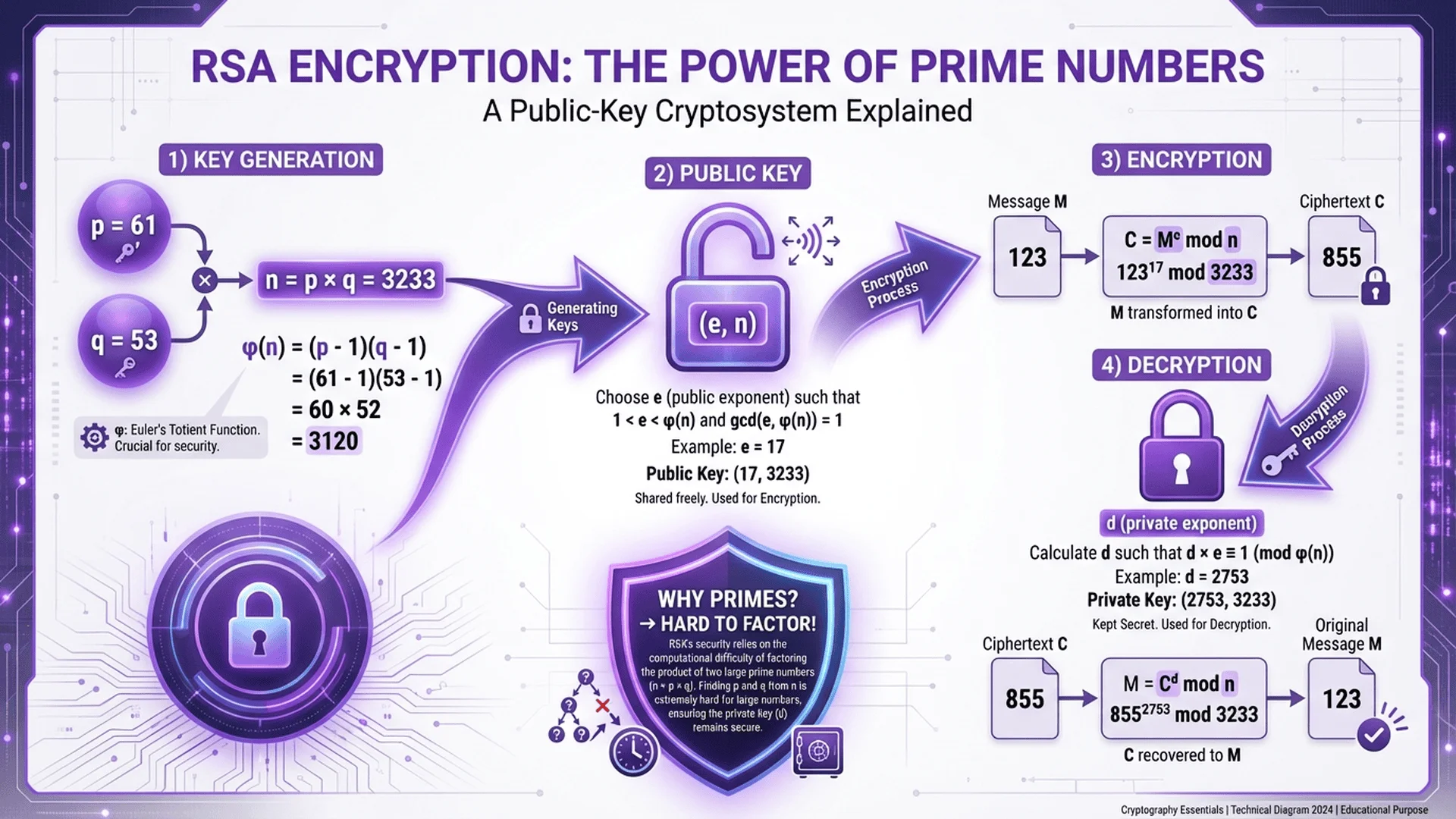
RSA Encryption: Primes Secure the Internet (1977)
The breakthrough: Rivest, Shamir, and Adleman invent public-key cryptography based on the difficulty of factoring large composite numbers.
How RSA works (simplified):
- Choose two large primes p and q (e.g., 1024 bits each)
- Multiply them: n = p × q (this is your public key modulus)
- Compute φ(n) = (p-1)(q-1) (Euler's totient)
- Choose encryption exponent e (typically 65537)
- Compute decryption exponent d = e^(-1) mod φ(n) (this is secret!)
Public key: (n, e) — anyone can encrypt with this
Private key: (d, p, q) — only you can decrypt
The security: Given n, finding p and q is extremely hard (no efficient classical algorithm). But if you know p and q, decryption is instant.
Example (tiny numbers for illustration):
Choose primes: p = 61, q = 53
n = 61 × 53 = 3233
φ(n) = (61-1)(53-1) = 60 × 52 = 3120
e = 17 (chosen such that gcd(17, 3120) = 1)
d = 2753 (computed via extended Euclidean algorithm)
Public key: (3233, 17)
Private key: (3233, 2753)
Encrypt message m=123:
c = 123^17 mod 3233 = 855
Decrypt ciphertext c=855:
m = 855^2753 mod 3233 = 123 ✓
Real-world RSA: Uses 2048-bit or 4096-bit keys (617-1234 digit primes). See our large prime generation guide for implementation details.
Impact: RSA (and variants) secure:
- HTTPS (green padlock in browsers)
- SSH (secure server access)
- PGP/GPG (email encryption)
- Bitcoin (transaction signatures)
- WhatsApp/Signal (end-to-end encryption)
Market value: The global cybersecurity market (heavily based on prime-powered crypto) was worth $173 billion in 2023 and growing 12% annually.
Primes in Nature: The 13 and 17-Year Cicadas
Biological mystery: North American periodical cicadas emerge every 13 or 17 years—both prime numbers. Coincidence?
The hypothesis: Prime-numbered cycles minimize overlap with predators or competing species that have shorter cycles.
Mathematical proof:
- Suppose a predator has a 5-year cycle
- A 13-year cicada overlaps with predator only every 13 × 5 = 65 years
- A 12-year cicada (composite) would overlap every 12 years (much more frequent!)
Specific example:
13-year cicada vs 5-year predator:
Overlap years: 65, 130, 195, 260, 325...
12-year cicada vs 5-year predator:
Overlap years: 60, 120, 180, 240, 300...
Difference: 13-year cicada has 21% fewer dangerous encounters!
Other prime patterns in nature:
- Sunflower seed spirals: Often have 34, 55, 89 seeds (Fibonacci numbers related to primes)
- Pinecone scales: Follow similar patterns
- Starfish arms: Some species have 5, 7, or 11 arms (all prime)
Why it works: Evolution favors patterns that avoid resonance with other cycles. Prime numbers naturally resist periodic overlap—a mathematical advantage in biological competition.
Hash Tables & Computer Science (1953 - Present)
Prime numbers power efficient data structures:
Hash table sizing: Best performance when table size is prime (reduces collisions).
Why? Consider storing 1000 items in a hash table:
Size = 1024 (2^10, composite):
- Many keys collide (divisors of 1024: 1,2,4,8,16,32...)
- Clustering occurs
- Performance degrades
Size = 1021 (prime):
- Collisions more evenly distributed
- No divisor patterns
- Better performance
Real-world use: Python's dict, Java's HashMap, C++'s unordered_map all use prime-based sizing strategies.
Random number generation: Linear congruential generators use large primes as moduli:
# Common LCG formula
next_value = (a × current_value + c) mod m
# 'm' is chosen as a large prime for best randomness
# Example: m = 2^31 - 1 = 2,147,483,647 (Mersenne prime M_31)
🚀 Explore Prime Number Tools
| Tool | Use Case | Technology |
|---|---|---|
| Prime Number Checker | Verify primes up to 18 digits | 6k±1 algorithm + BigInt |
| Hash Generator | Generate SHA-256 hashes (like in Bitcoin) | Prime-based crypto |
| Random Generator | Cryptographically secure random numbers | Prime-modulus LCG |
Learn the Algorithms Behind the History:
- Python Tutorial — Implement Sieve of Eratosthenes
- Algorithm Comparison — Fermat vs Miller-Rabin vs AKS
- Large Prime Detection — Generate RSA-grade primes
💡 Did You Know? The algorithms you learned about (Euclidean, Sieve, Fermat) are all implemented in our tools. Check our technical documentation to see the actual code!
👉 Try Free Prime Checker Now →
Part 4 - Modern Frontiers & Future Directions (2002 - 2025+)
AKS Algorithm: Primes are in P (2002)
The breakthrough: Manindra Agrawal, Neeraj Kayal, and Nitin Saxena proved that primality testing is in polynomial time (complexity class P).
Why revolutionary: Before AKS, we had:
- Deterministic but slow: Trial division (exponential time)
- Fast but probabilistic: Miller-Rabin (tiny error chance)
AKS delivers: Deterministic AND polynomial time → O(log^6 n) in the number of digits, not the value!
The catch: Despite polynomial complexity, AKS is slower than Miller-Rabin for all practical input sizes (even 10,000-digit numbers).
Comparison (1024-bit prime):
- Miller-Rabin (k=40 rounds): ~50-200ms
- AKS original: ~30 minutes
- AKS optimized: ~5 minutes
Impact: Theoretical masterpiece (proves P contains primality), but Miller-Rabin remains the practical choice. AKS variants are used in mathematical research when proof (not just probability) is required.
Quantum Computing: Threat and Opportunity
Shor's Algorithm (1994): Quantum computers can factor large numbers in polynomial time, breaking RSA encryption.
The threat:
Classical computer factoring 2048-bit RSA:
~300 trillion years
Quantum computer (with Shor's algorithm):
~8 hours (estimated for future 4000-qubit machine)
Current status (2025):
- Largest number factored by quantum computer: 21 (= 3 × 7) using 5 qubits
- Breaking RSA-2048 requires ~4000 error-corrected qubits
- Best quantum computers today: ~1000 qubits (error-prone)
- Estimated timeline: 10-20 years before RSA is truly threatened
Post-quantum cryptography: NIST standardized quantum-resistant algorithms in 2024:
- Lattice-based crypto (Kyber, Dilithium) — No primes needed!
- Hash-based signatures (SPHINCS+)
- Code-based crypto (McEliece)
Irony: Quantum computers threaten prime-based encryption but don't significantly speed up primality testing. Prime checking remains secure!
The Great Internet Mersenne Prime Search (GIMPS)
Distributed computing at scale:
- Launched: 1996
- Participants: 1.9 million CPUs worldwide
- Discoveries: 17 Mersenne primes (including the current record)
- Prize: $150,000 from Electronic Frontier Foundation for first 100-million-digit prime
How it works:
1. Download GIMPS software (Prime95)
2. Software tests Mersenne prime candidates during CPU idle time
3. Coordinate with central server to avoid duplicate work
4. If you find a new record, you win fame + prize money!
Current search status:
- All exponents up to ~110,000,000 tested
- Next Mersenne prime (if it exists) will have 30+ million digits
- Estimated: 2-5 years until next discovery (probabilistic)
Join the hunt: Download Prime95 from https://www.mersenne.org/ and contribute your spare CPU cycles!
Unsolved Mysteries & Open Questions
Despite 2,300 years of study, fundamental questions remain:
1. Twin Prime Conjecture
- Claim: Infinitely many "twin primes" (primes differing by 2, e.g., 11 & 13, 17 & 19)
- Status: Unproven! (Though Yitang Zhang proved gaps ≤ 70 million in 2013, later improved to gaps ≤ 246)
2. Goldbach's Conjecture
- Claim: Every even number > 2 is the sum of two primes (e.g., 10 = 3 + 7, 100 = 47 + 53)
- Status: Verified for all numbers up to 4 × 10^18, but no proof exists
3. Riemann Hypothesis
- Claim: All non-trivial zeros of the Riemann zeta function lie on the critical line Re(s) = 1/2
- Why it matters: Relates to distribution of primes among integers
- Prize: $1 million from Clay Mathematics Institute
- Status: One of the most important unsolved problems in mathematics
4. Prime Formula
- Question: Is there a polynomial formula that generates only primes?
- Status: No simple formula exists (though complex constructions exist)
These mysteries keep thousands of mathematicians employed and fuel ongoing discoveries!
Conclusion: Primes Past, Present, and Future
A Timeline of Prime Number Milestones
| Year | Breakthrough | Impact |
|---|---|---|
| 300 BCE | Euclid proves infinitude | Establishes primes as fundamental |
| 240 BCE | Eratosthenes' sieve | First algorithm to generate primes |
| 1640 | Fermat's Little Theorem | Enables fast primality testing |
| 1644 | Mersenne investigates 2^p - 1 | Begins hunt for giant primes |
| 1949 | ENIAC verifies M_127 | Computers enter prime research |
| 1977 | RSA encryption invented | Primes become worth trillions |
| 2002 | AKS proves primes in P | Theoretical milestone |
| 2018 | M_82,589,933 discovered | Current largest known prime |
| 2024 | Post-quantum crypto standardized | Preparing for quantum future |
Why Primes Still Matter in 2025
Economic impact:
- Cybersecurity industry: $173 billion annually (2023)
- E-commerce protected by RSA: Trillions in transactions
- Blockchain/crypto: $1+ trillion market cap secured by prime-based signatures
Scientific frontiers:
- Quantum computing research: Understanding post-quantum security
- Distributed computing: GIMPS unites millions in shared mathematical quest
- AI/machine learning: Prime-based hashing in neural network architectures
Educational value:
- Entry point to number theory: Simple concept, infinite depth
- Algorithmic thinking: From Sieve to Miller-Rabin teaches optimization
- Proof techniques: Euclid's infinitude is still a teaching masterpiece
The Next 100 Years: Predictions
Near-term (2025-2035):
- Quantum computers break RSA-2048 (timeline uncertain, but preparations underway)
- Post-quantum crypto adoption: Migration to lattice/hash-based systems
- 100-million-digit prime discovered: GIMPS continues march to larger Mersenne primes
Medium-term (2035-2075):
- Twin Prime Conjecture solved? (50/50 chance, according to mathematicians)
- Goldbach's Conjecture proven? (Many believe this will fall within 50 years)
- New prime applications: Quantum algorithms may use primes in unexpected ways
Long-term (2075-2125):
- Riemann Hypothesis resolved: Impact on prime distribution understanding
- Biological prime applications: Engineered organisms using prime-cycle optimization
- Interstellar communication: Primes as universal "hello" signal (already used in SETI)
Wild speculation: If we encounter alien civilizations, prime numbers will likely be among the first mathematical concepts we recognize in common—they're universal, independent of base systems or notation. The Voyager Golden Record included prime numbers as part of our "introduction to Earth."
Your Prime Number Journey Starts Here
Whether you're a student tackling homework, a developer implementing cryptography, or a curious mind exploring mathematics, prime numbers offer endless fascination.
Get hands-on:
- Check any prime instantly with our free tool
- Learn algorithms from Sieve to Miller-Rabin
- Generate cryptographic primes for real applications
- Compare implementations in Python, Java, JavaScript, C
From Euclid's geometric proof to quantum-resistant cryptography, prime numbers bridge ancient wisdom and cutting-edge technology. They've secured empires, encrypted revolutions, and will protect digital civilization for decades to come.
The quest continues: Join the millions searching for the next Mersenne prime, or simply appreciate that every "https://" in your browser is a testament to 2,300 years of mathematical progress. Primes aren't just numbers—they're humanity's longest-running intellectual adventure.
Frequently Asked Questions
1. Who discovered prime numbers?
Short answer: No single person "discovered" primes—they're a natural property of numbers that ancient civilizations recognized independently.
Detailed history:
Ancient Egypt (~1650 BCE):
- The Rhind Mathematical Papyrus shows Egyptians understood that some numbers (like 2, 3, 5, 7) had "special" divisibility properties
- No evidence they formalized the concept or named them "primes"
Ancient Greece (~500 BCE):
- Pythagoras and followers (500 BCE) studied number properties, likely knew about primes
- Euclid (300 BCE) formalized the concept in Elements (Book VII, Definition 11):
"A prime number is that which is measured by a unit alone"
- Euclid's Proposition 20: Proved infinitude of primes (first major theorem!)
Ancient China (~200 BCE):
- Chinese mathematicians independently studied primes in connection with astronomy
- The Nine Chapters mentions "indivisible numbers"
India (~500 CE):
- Aryabhata worked with primes in astronomical calculations
- Used primes in calendar systems
Credit: While many cultures discovered primes, Euclid gets credit for:
1. Formal definition
2. First major proof (infinitude)
3. Systematic study in Elements (still taught today!)
Modern terminology:
- The word "prime" comes from Latin primus (first, primary)
- Reflects their role as "first" numbers from which all others are built
Fun fact: Euclid wouldn't recognize modern notation (he used Greek letters and geometric language), but his proof structure is identical to what we teach in 2025!
2. How are prime numbers used in real life?
Primes are everywhere in modern technology—you used them multiple times just to read this article:
1. Internet Security (Most Critical Application)
Every "https://" connection:
You visit https://amazon.com
↓
Your browser and Amazon's server perform RSA handshake
↓
Exchange encryption keys (generated from 2048-bit primes)
↓
All data encrypted using those keys
↓
Your credit card info is safe ✓
Scale: Trillions of RSA handshakes happen daily across the internet. Without primes, online banking, shopping, and email would be impossible to secure.
Examples:
- TLS/SSL certificates: Your browser verifies website identity using prime-based signatures
- VPNs: Encrypt your traffic using prime-powered algorithms
- WhatsApp/Signal: End-to-end encryption uses primes for key generation
2. Blockchain & Cryptocurrency
Bitcoin transactions:
You send Bitcoin to someone
↓
Sign transaction with private key (derived from primes)
↓
Network verifies signature using your public key
↓
Transaction added to blockchain ✓
Ethereum, Litecoin, and nearly all cryptocurrencies use Elliptic Curve Cryptography (which relies on prime-order groups).
Market impact: $1+ trillion cryptocurrency market cap secured by prime-based math.
3. Computer Science & Programming
Hash tables:
# Python dict implementation uses prime-sized tables
my_dict = {'apple': 1, 'banana': 2, 'cherry': 3}
# Internal size: 8 (2^3) → bad performance
# Python automatically resizes to prime: 11 → better distribution!
Random number generation:
// Linear Congruential Generator (used in many systems)
next_random = (multiplier × seed + increment) % modulus
// 'modulus' is chosen as large prime (e.g., 2^31 - 1)
// Ensures maximal period and good randomness
Load balancing: Servers use prime-numbered consistent hashing to distribute requests evenly.
4. Nature & Biology
Cicada life cycles:
- 13-year and 17-year periodical cicadas (both prime!)
- Minimizes overlap with predators/competitors
- Evolution discovered primes before humans did!
Genetic algorithms:
- Prime-numbered mutation rates avoid resonance patterns
- Used in AI/ML optimization
5. Everyday Hidden Uses
Credit card verification:
- Luhn algorithm (checksum) uses modular arithmetic related to primes
- Detects typos when you enter card numbers
Barcode readers:
- Reed-Solomon error correction (uses prime fields)
- Allows scanners to read damaged barcodes
GPS systems:
- Satellite signals use prime-based spreading codes
- Enables multiple satellites to transmit simultaneously without interference
QR codes:
- Error correction based on prime-order finite fields
- Why QR codes work even when partially obscured
Bottom line: If you've done any of these today, you've relied on primes:
- ✅ Visited an https:// website
- ✅ Sent an encrypted message
- ✅ Made an online purchase
- ✅ Used a dictionary/map data structure (programming)
- ✅ Scanned a QR code
- ✅ Used GPS navigation
Primes aren't just abstract math—they're the invisible infrastructure of digital civilization!
3. What is the largest known prime number?
Current record (as of January 2025):
M_82,589,933 = 2^82,589,933 - 1
Statistics:
- Decimal digits: 24,862,048 (nearly 25 million!)
- Discovered: December 7, 2018
- Discoverer: Patrick Laroche (GIMPS volunteer, Ocala, Florida)
- Computer used: Intel i5-4590 CPU @ 3.30GHz
- Computation time: 12 days of continuous calculation
- Verification: Independently verified by 4 different computers
How big is 24,862,048 digits?
- Book pages: ~10,000 pages (if printed at 2,500 digits/page)
- File size: ~24 MB as plain text
- Reading time: ~3-4 weeks nonstop at 2 digits/second
- Comparison: 3 million times more digits than 2^1024 (common RSA key size)
All-Time Top 10 Largest Known Primes (all Mersenne primes):
| Rank | Prime | Digits | Discovery Date |
|---|---|---|---|
| 1 | 2^82,589,933 - 1 | 24,862,048 | Dec 2018 |
| 2 | 2^77,232,917 - 1 | 23,249,425 | Dec 2017 |
| 3 | 2^74,207,281 - 1 | 22,338,618 | Jan 2016 |
| 4 | 2^57,885,161 - 1 | 17,425,170 | Jan 2013 |
| 5 | 2^43,112,609 - 1 | 12,978,189 | Aug 2008 |
| 6 | 2^42,643,801 - 1 | 12,837,064 | Jun 2009 |
| 7 | 2^37,156,667 - 1 | 11,185,272 | Sep 2008 |
| 8 | 2^32,582,657 - 1 | 9,808,358 | Sep 2006 |
| 9 | 2^30,402,457 - 1 | 9,152,052 | Dec 2005 |
| 10 | 2^25,964,951 - 1 | 7,816,230 | Feb 2005 |
Notice: All discovered by GIMPS (Great Internet Mersenne Prime Search) distributed computing project!
Why are all record primes Mersenne primes?
- Faster testing: Lucas-Lehmer test is much faster than general Miller-Rabin for numbers of form 2^p - 1
- Systematic search: Can test in order (p = 2, 3, 5, 7, 11, 13...) unlike random prime hunting
- Community effort: GIMPS coordinates 1.9 million CPUs worldwide
Next milestone: $150,000 prize from Electronic Frontier Foundation for first 100-million-digit prime (likely M_p where p ≈ 332,000,000).
Estimated timeline: 2-10 years, depending on luck and computational power growth.
Join the search: Download Prime95 from https://www.mersenne.org/ and help find the next record!
4. Why are prime numbers important in cryptography?
Prime numbers are the foundation of modern internet security due to a mathematical asymmetry: multiplying primes is easy, factoring their product is (currently) impossible at scale.
The Core Principle: One-Way Functions
Easy direction (multiplication):
p = 9,007,199,254,740,881 (prime)
q = 9,007,199,254,740,643 (prime)
n = p × q = 81,129,638,414,606,663,814,578,607,183
(takes <1 microsecond on any computer)
Hard direction (factorization):
Given: n = 81,129,638,414,606,663,814,578,607,183
Find: p and q such that p × q = n
Using best classical algorithms:
- Trial division: ~10^13 years
- General Number Field Sieve: ~1 million years (for this 63-bit example)
For 2048-bit RSA keys:
Product n: 617 decimal digits
Factoring time (classical): 300 trillion years (current estimates)
Factoring time (quantum, future): ~8 hours (Shor's algorithm)
Why This Matters for RSA Encryption
Public key (n, e): Anyone can encrypt with this → safe to share
Private key (d, p, q): Only you can decrypt → must stay secret
Security guarantee: Recovering private key from public key requires factoring n into p and q, which is computationally infeasible.
Example (tiny numbers for illustration):
Alice generates keys:
p = 61, q = 53
n = 3,233 (public)
d = 2,753 (secret)
Bob encrypts message m=123:
c = 123^17 mod 3,233 = 855 (sends to Alice)
Attacker sees:
n = 3,233 (public)
c = 855 (intercepted)
To decrypt, attacker needs to:
1. Factor 3,233 = 61 × 53 (easy for tiny numbers!)
2. Compute d from p and q
3. Decrypt: 855^d mod 3,233 = 123
For real RSA (2048-bit):
Factoring n takes 300 trillion years → attacker gives up
Other Prime-Based Crypto Primitives
Diffie-Hellman Key Exchange:
Public: large prime p and generator g
Alice secret: a (random)
Bob secret: b (random)
Alice sends: g^a mod p
Bob sends: g^b mod p
Shared key: g^(ab) mod p (both compute without revealing a or b)
Why secure: Computing g^a from g and g^(ab) requires solving discrete logarithm problem (hard when p is prime).
Digital Signatures (DSA, ECDSA):
- Use prime-order groups for signing/verification
- Security relies on difficulty of discrete log in prime fields
Elliptic Curve Cryptography:
- Works over fields of prime order
- Same security as RSA with shorter keys (256-bit ECC ≈ 3072-bit RSA)
The Quantum Threat
Shor's Algorithm (1994): Quantum computers can factor n into p × q in polynomial time.
Timeline:
- Today (2025): Largest number factored quantumly: 21 = 3 × 7
- ~2030-2040: Quantum computers may break RSA-2048
- Countermeasure: Post-quantum crypto (lattice-based, hash-based) doesn't use primes!
Ironic: Primes built modern cryptography and will be retired by quantum computing—but primality testing itself remains secure (quantum speedup is minimal).
Bottom line: Primes enable public-key cryptography, the technology that makes secure internet possible. The mathematical gap between easy multiplication and hard factorization is the foundation of digital trust in 2025.
Learn to implement RSA yourself in our large prime detection guide or explore the algorithms in our comparison guide.
References
- Euclid - Elements, Book VII and IX (300 BCE), available in modern translation from Dover Publications
- Ribenboim, Paulo - The Little Book of Bigger Primes (2004), Springer
- Crandall, Richard & Pomerance, Carl - Prime Numbers: A Computational Perspective (2005), Springer
- Rivest, Shamir, Adleman - "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems" (1978)
- Agrawal, Kayal, Saxena - "PRIMES is in P" (2002): https://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf
- GIMPS - Great Internet Mersenne Prime Search: https://www.mersenne.org/
- OEIS - Prime Number Database: https://oeis.org/A000040
- NIST Post-Quantum Cryptography Standards (2024): https://csrc.nist.gov/projects/post-quantum-cryptography
- Shor, Peter - "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer" (1994)
- Electronic Frontier Foundation - Cooperative Computing Awards: https://www.eff.org/awards/coop