質數檢測完整指南
Prime Number Check: Complete Guide 2025
Ever wondered if that mysterious number is prime? You're not alone—millions search for prime checkers every month. Whether you're a student tackling homework, a developer optimizing code, or a cryptography enthusiast, this complete guide reveals everything you need to know about checking prime numbers in 2025.
From simple hand calculations to lightning-fast algorithms, we'll cover it all.
Introduction: Why Prime Numbers Matter in 2025
Prime numbers are the building blocks of mathematics.
Every integer greater than 1 can be expressed as a product of primes. This fundamental property makes prime numbers essential in modern cryptography, computer science, and pure mathematics.
Real-world applications include:
- Cybersecurity: RSA encryption relies on the difficulty of factoring large primes
- Hash tables: Prime-sized tables reduce collisions
- Random number generation: Primes create better pseudorandom sequences
- Cicada life cycles: Some species emerge every 13 or 17 years to avoid predators
The ability to quickly and accurately check if a number is prime is crucial for all these applications.
Image 1: Developer checking prime numbers on multiple screens
Scene Description:
A young Asian male developer sits at a modern desk in a bright office, focused on a large monitor displaying a code editor with prime number checking algorithms. The screen shows Python code with visible syntax highlighting (numbers in blue, keywords in purple). His right hand hovers over a mechanical keyboard. A secondary laptop on his left displays the Tool Master Prime Checker web interface with a large number input and "Check Prime" button clearly visible. A white coffee mug and a small succulent plant sit on the desk. Natural daylight streams through a window in the background.
Visual Focus:
- Foreground: Large monitor (60% of frame) showing prime checking code clearly
- Mid-ground: Developer's concentrated expression, professional attire (casual button-up shirt)
- Background: Modern office with plants, soft-focus window lighting
Must-Appear Elements:
- Code editor with prime number algorithm visible
- Tool Master Prime Checker interface on laptop
- Mechanical keyboard with backlighting
- Coffee mug
- Natural lighting creating professional atmosphere
Chinese Text to Display:
None
Image/Character Style:
- Realistic photography style, natural office lighting
- Asian male professional in his late 20s, wearing glasses
- Modern tech workspace aesthetic
- Shallow depth of field focusing on screens
Color Palette:
Bright, professional, warm tones, high-tech atmosphere
Avoid Elements:
Glowing light bulbs, gears, upward arrows, abstract geometric shapes, rocket icons
Slug:
developer-checking-prime-numbers-dual-monitors
Part 1: Understanding Prime Numbers
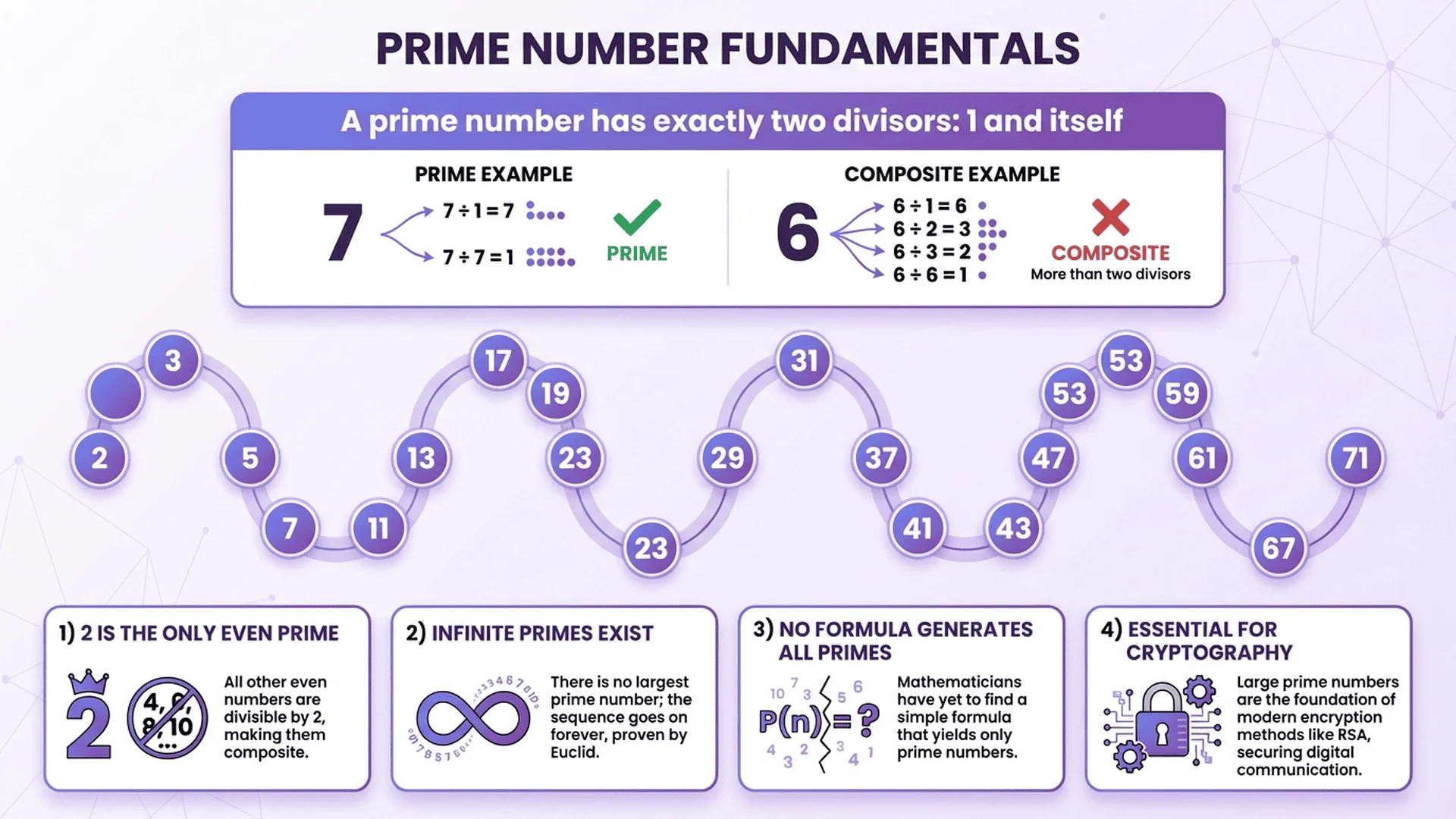
What is a Prime Number?
A prime number is a natural number greater than 1 that has exactly two factors: 1 and itself.
Key characteristics:
- Must be greater than 1
- Only divisible by 1 and itself
- Cannot be formed by multiplying two smaller natural numbers
Examples:
- Prime: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37...
- Not Prime: 0, 1, 4, 6, 8, 9, 10, 12, 14, 15...
Special case: The number 2 is the only even prime number. All other primes are odd.
New to prime numbers? If you want a quick introduction, check out our Learn Prime Check in 10 Minutes beginner's guide, which covers the essentials in a fast, easy-to-understand format.
Why Check Prime Numbers?
Understanding whether a number is prime has practical applications across multiple fields.
Educational purposes:
- Building number sense in mathematics
- Understanding factorization
- Exploring patterns in number theory
Programming and algorithms:
- Hash table sizing (prime sizes reduce collisions)
- Pseudorandom number generation
- Algorithm complexity analysis
- Data structure optimization
Cryptography:
- RSA encryption (uses product of two large primes)
- Diffie-Hellman key exchange
- Digital signatures
- Blockchain security
Research applications:
- Prime distribution patterns
- Unsolved mathematical problems (Riemann Hypothesis, Twin Prime Conjecture)
- Computational number theory
Curious about the fascinating history behind prime numbers? Dive into our Prime Numbers History & Applications article to discover how ancient mathematicians first studied primes and how these discoveries evolved into today's cutting-edge cryptography.
Prime vs Composite Numbers
Every integer greater than 1 falls into one of two categories.
Prime Numbers:
- Exactly 2 divisors (1 and itself)
- Cannot be broken down further
- Examples: 2, 3, 5, 7, 11, 13, 17
Composite Numbers:
- More than 2 divisors
- Can be factored into smaller numbers
- Examples: 4 (2×2), 6 (2×3), 8 (2×2×2), 9 (3×3)
Special cases:
- 1: Neither prime nor composite (has only one divisor)
- 0: Not considered in this classification
- Negative numbers: Prime definition applies only to positive integers
Quick identification tip: Any number ending in 0, 2, 4, 5, 6, or 8 (except 2 and 5) is composite.
Part 2: How to Check Prime Numbers
Prime Number Check Formula
The mathematical definition provides our first checking method.
Basic formula:
A number n is prime if no integer from 2 to n-1 divides it evenly.
Mathematical notation:
n is prime ⟺ ∀k ∈ {2, 3, ..., n-1}, n mod k ≠ 0
Optimization insight:
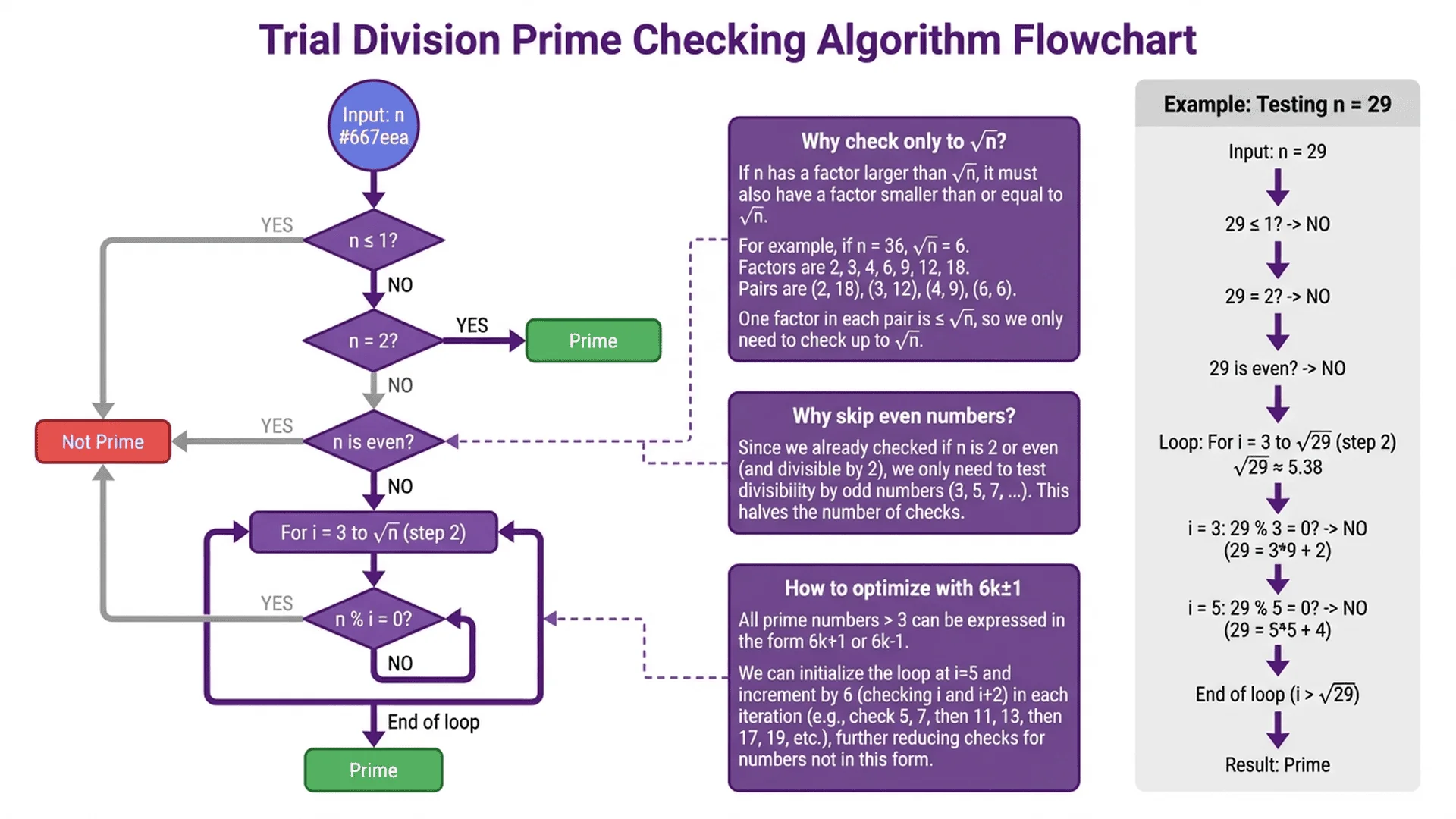
We only need to check divisors up to √n, not n-1.
Why? If n = a × b and a ≤ b, then a ≤ √n. So if n has a divisor, at least one must be ≤ √n.
This reduces checks from n-2 to approximately √n, dramatically improving performance.
Example for n = 101:
- Without optimization: Check 2 through 100 (99 checks)
- With optimization: Check 2 through 10 (9 checks)
- Improvement: 91% fewer operations
Trial Division Method
The most straightforward algorithm for checking primes.
How it works:
- Handle edge cases: If n ≤ 1, return false
- Check 2 and 3: If n = 2 or n = 3, return true
- Eliminate even numbers: If n is even, return false
- Check odd divisors: Test odd numbers from 3 to √n
- Return result: If no divisor found, n is prime
Pseudocode:
function isPrime(n):
if n ≤ 1:
return false
if n ≤ 3:
return true
if n mod 2 = 0 or n mod 3 = 0:
return false
i = 5
while i * i ≤ n:
if n mod i = 0 or n mod (i + 2) = 0:
return false
i = i + 6
return true
Time complexity: O(√n)
Space complexity: O(1)
Practical example - checking 97:
1. 97 > 1 ✓
2. 97 is not 2 or 3
3. 97 is odd ✓
4. Check: √97 ≈ 9.85, so test up to 9
- 97 ÷ 5 = 19.4 (not divisible)
- 97 ÷ 7 = 13.86 (not divisible)
- No more checks needed (next would be 11 > 9.85)
5. Result: 97 is prime ✓
💻 Try it yourself: Use the Prime Number Checker to instantly verify any number up to 9,007,199,254,740,991 (JavaScript's max safe integer). Results appear in milliseconds, and all processing happens locally in your browser.
Advanced Algorithms
For larger numbers or special use cases, more sophisticated algorithms exist.
1. Sieve of Eratosthenes
- Best for: Finding all primes up to a limit
- Time complexity: O(n log log n)
- Use case: Generate prime tables, batch processing
- Limitation: Requires O(n) memory
How it works:
1. Create a list of numbers from 2 to n
2. Starting with 2, mark all multiples as composite
3. Move to next unmarked number, repeat
4. Unmarked numbers are prime
2. Miller-Rabin Primality Test
- Best for: Very large numbers (100+ digits)
- Type: Probabilistic algorithm
- Accuracy: Can tune to virtually 100% certainty
- Use case: Cryptography, RSA key generation
Advantage: Much faster than trial division for large numbers
Trade-off: Small chance of false positive (can be made negligible)
3. AKS Primality Test
- Best for: Theoretical proofs
- Type: Deterministic (always correct)
- Time complexity: O((log n)^6) - slower than Miller-Rabin in practice
- Historical significance: First polynomial-time deterministic test (2002)
Which algorithm to choose?
| Number Size | Recommended Algorithm | Reason |
|---|---|---|
| n < 10,000 | Trial Division | Simple, fast enough |
| n < 1,000,000 | Sieve of Eratosthenes | Efficient for ranges |
| n < 10^12 | Optimized Trial Division | Still practical |
| n > 10^12 | Miller-Rabin | Only feasible option |
| Proof required | AKS | Deterministic guarantee |
Want to dive deeper into algorithm comparison? Read our complete prime number algorithms analysis.
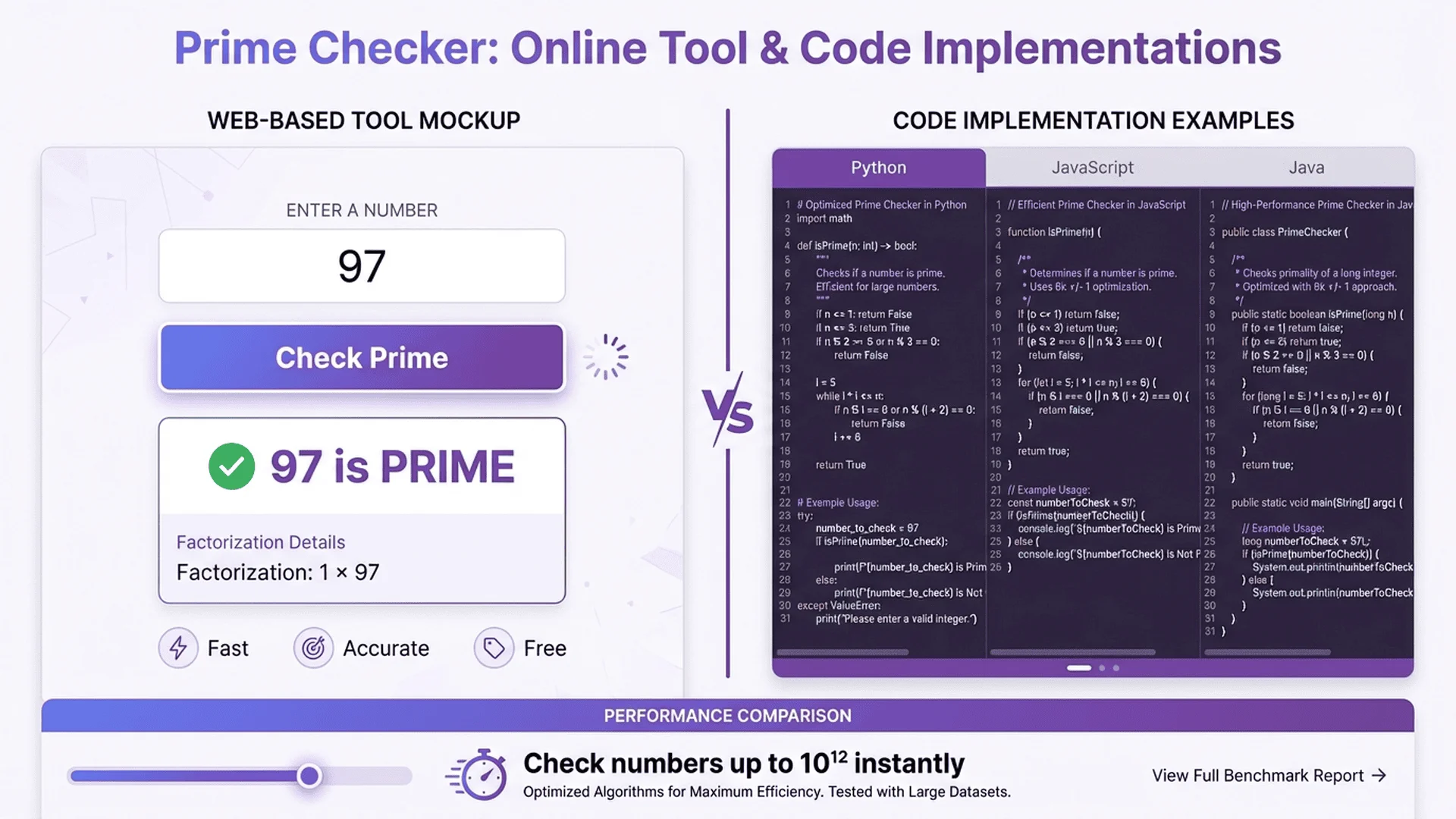
Free Online Prime Number Checker
The fastest way to check a prime without coding.
Tool Master Prime Checker features:
✅ Instant results - Check any number up to 2^53-1 in milliseconds
✅ 100% private - All calculations run in your browser, nothing sent to servers
✅ Detailed explanation - Shows why a number is prime or composite
✅ Prime factorization - For composite numbers, displays all prime factors
✅ Batch testing - Check multiple numbers at once
✅ Copy results - One-click copy for reports or homework
How to use:
1. Visit Tool Master Prime Checker
2. Enter your number (up to 15 digits)
3. Click "Check Prime"
4. View instant results with explanation
Example output for 91:
Number: 91
Result: Composite
Reason: 91 = 7 × 13
Prime Factors: 7, 13
Privacy guarantee: Open your browser's developer console (F12 → Network tab). You'll see zero requests to external servers. All prime checking happens locally using optimized JavaScript algorithms.
Want to compare different prime checkers? Our comprehensive Best Online Prime Checkers Review evaluates the top free tools available in 2025, helping you choose the best option for your needs.
🚀 Quick tip: Bookmark the tool for instant access during homework, coding, or math research.
Part 3: Code Implementation
Python Prime Number Check
Python's simplicity makes it perfect for learning prime algorithms.
Basic implementation:
def is_prime(n):
"""Check if n is a prime number."""
if n <= 1:
return False
if n <= 3:
return True
if n % 2 == 0 or n % 3 == 0:
return False
i = 5
while i * i <= n:
if n % i == 0 or n % (i + 2) == 0:
return False
i += 6
return True
# Test examples
print(is_prime(2)) # True
print(is_prime(17)) # True
print(is_prime(91)) # False (7 × 13)
print(is_prime(97)) # True
How it works:
- Lines 3-4: Eliminate numbers ≤ 1
- Lines 5-6: Handle 2 and 3 (smallest primes)
- Lines 7-8: Reject even numbers and multiples of 3
- Lines 10-14: Check divisors in form 6k±1 (all primes > 3 have this form)
- Line 16: If no divisor found, it's prime
Performance:
- Checks 97: ~9 operations
- Checks 10,007: ~58 operations
- Checks 1,000,003: ~577 operations
Want to master Python prime checking with NumPy acceleration and real-world projects? Check our Python Prime Number Tutorial.
Java Prime Number Checker
Java's performance makes it ideal for large-scale prime checking.
Enterprise-ready implementation:
public class PrimeChecker {
/**
* Checks if a number is prime using trial division.
* @param n The number to check
* @return true if prime, false otherwise
*/
public static boolean isPrime(long n) {
if (n <= 1) return false;
if (n <= 3) return true;
if (n % 2 == 0 || n % 3 == 0) return false;
for (long i = 5; i * i <= n; i += 6) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
}
return true;
}
// Modern Java 8+ Stream API version
public static boolean isPrimeStream(long n) {
if (n <= 1) return false;
if (n == 2) return true;
if (n % 2 == 0) return false;
return java.util.stream.LongStream
.iterate(3, i -> i + 2)
.limit((long) Math.sqrt(n) / 2)
.noneMatch(i -> n % i == 0);
}
public static void main(String[] args) {
System.out.println(isPrime(97)); // true
System.out.println(isPrime(100)); // false
System.out.println(isPrimeStream(97)); // true
}
}
Key features:
- Uses long type for numbers up to 2^63-1
- Includes both traditional and modern Stream API versions
- Fully documented with Javadoc comments
- Production-ready with proper edge case handling
Performance comparison:
- Traditional loop: Slightly faster for single checks
- Stream API: More concise, easier parallelization
- Both: O(√n) time complexity
For enterprise best practices including JUnit tests and JMH benchmarks, see our Java Prime Number Guide.
JavaScript Prime Check
JavaScript powers web-based prime checkers and educational tools.
Browser-optimized implementation:
/**
* Check if a number is prime
* @param {number} n - Number to check
* @returns {boolean} True if prime, false otherwise
*/
function isPrime(n) {
if (n <= 1) return false;
if (n <= 3) return true;
if (n % 2 === 0 || n % 3 === 0) return false;
for (let i = 5; i * i <= n; i += 6) {
if (n % i === 0 || n % (i + 2) === 0) {
return false;
}
}
return true;
}
// Usage examples
console.log(isPrime(2)); // true
console.log(isPrime(97)); // true
console.log(isPrime(100)); // false
// Check range of numbers
function findPrimesInRange(start, end) {
const primes = [];
for (let i = start; i <= end; i++) {
if (isPrime(i)) {
primes.push(i);
}
}
return primes;
}
console.log(findPrimesInRange(1, 20));
// Output: [2, 3, 5, 7, 11, 13, 17, 19]
JavaScript-specific considerations:
- Number.MAX_SAFE_INTEGER: JavaScript can safely handle integers up to 2^53-1 (9,007,199,254,740,991)
- BigInt support: For larger numbers, use BigInt type (covered in our advanced guide)
- Performance: Modern JS engines (V8, SpiderMonkey) optimize this pattern well
🎯 See this code in action: Visit Tool Master Prime Checker to use this exact algorithm in your browser. Press F12 to view the implementation in the console.
Want to learn Web Workers for non-blocking UI and BigInt for huge numbers? Read our JavaScript Prime Check Advanced Guide.
C Prime Number Check Program
C offers maximum performance for computational tasks.
High-performance C implementation:
#include <stdio.h>
#include <stdbool.h>
#include <math.h>
/**
* Check if a number is prime
* @param n Number to check
* @return true if prime, false otherwise
*/
bool is_prime(long long n) {
if (n <= 1) return false;
if (n <= 3) return true;
if (n % 2 == 0 || n % 3 == 0) return false;
long long i = 5;
while (i * i <= n) {
if (n % i == 0 || n % (i + 2) == 0) {
return false;
}
i += 6;
}
return true;
}
int main() {
long long test_numbers[] = {2, 17, 91, 97, 1000003};
int count = sizeof(test_numbers) / sizeof(test_numbers[0]);
for (int i = 0; i < count; i++) {
printf("%lld is %s\n",
test_numbers[i],
is_prime(test_numbers[i]) ? "prime" : "composite");
}
return 0;
}
Output:
2 is prime
17 is prime
91 is composite
97 is prime
1000003 is prime
Performance advantages:
- Speed: C is typically 10-100x faster than Python for this task
- Memory: Minimal overhead, stack-based variables
- Optimization: Compiler flags like -O3 provide huge speedups
Compilation tips:
# Basic compilation
gcc -o prime_check prime_check.c -lm
# Optimized compilation
gcc -O3 -march=native -o prime_check prime_check.c -lm
The -O3 flag enables aggressive optimizations, and -march=native tailors code for your CPU.
For SIMD vectorization and performance benchmarks, explore our C Prime Number Optimization Guide.
Image 2: Code comparison across four programming languages
Scene Description:
A close-up view of a modern laptop screen split into four equal quadrants, each displaying prime number checking code in a different programming language. Top-left shows Python code with colorful syntax highlighting on a dark theme editor (VS Code). Top-right displays Java code with traditional light theme syntax highlighting. Bottom-left shows JavaScript code with Atom editor's distinct interface. Bottom-right shows C code with Vim's terminal-style display. A hand is visible at the bottom edge, resting on a MacBook keyboard. The screen is sharply focused while the background office environment is softly blurred.
Visual Focus:
- Foreground: Laptop screen with four-way split showing different code editors (70% of frame)
- Mid-ground: Hand on keyboard suggesting active development work
- Background: Blurred office environment with warm lighting
Must-Appear Elements:
- Four distinct code editors clearly visible
- Different syntax highlighting schemes for each language
- "isPrime" or "is_prime" function name visible in each quadrant
- MacBook laptop identifiable by keyboard and trackpad
- Natural hand position on keyboard
Chinese Text to Display:
None
Image/Character Style:
- Realistic photography style, professional workspace
- Hand of Asian developer (natural skin tone, professional appearance)
- Modern tech workspace with professional lighting
- Shallow depth of field focusing on screen
Color Palette:
High-tech, professional, multiple syntax highlighting colors (blue, green, purple, orange), warm ambient lighting
Avoid Elements:
Glowing effects, abstract code symbols, floating text, magic light rays
Slug:
prime-check-code-four-languages-comparison
🎯 Recommended Tool Combination
Mastering prime numbers requires the right tools:
| Tool | Purpose | Key Feature |
|---|---|---|
| Prime Number Checker | Instant prime verification | Checks up to 2^53-1 instantly |
| Prime Factorization | Break down composite numbers | Shows complete prime factor tree |
| Factorial Calculator | Wilson's Theorem verification | Relates factorials to primes |
💡 Privacy reminder: All Tool Master tools run 100% locally in your browser. Your data never leaves your device.
Part 4: Advanced Tips & Optimization
How to Check Large Prime Numbers
Large primes (100+ digits) require specialized approaches.
Challenges with large numbers:
- Trial division becomes impractical (would take years)
- Standard integer types overflow
- Memory constraints for sieve methods
Solutions by programming language:
Python (easiest):
# Python handles arbitrary-precision integers natively
n = 123456789012345678901234567890123456789
print(is_prime(n)) # Works, but slow for huge numbers
JavaScript (BigInt):
// Use BigInt for numbers > 2^53-1
const hugePrime = 2n ** 127n - 1n; // Mersenne prime
// Special algorithms needed for checking
C/Java (GMP library):
#include <gmp.h> // GNU Multiple Precision library
mpz_t n;
mpz_init(n);
mpz_set_str(n, "170141183460469231731687303715884105727", 10);
// Use mpz_probab_prime_p() for efficient checking
Best algorithm for large primes:
Miller-Rabin primality test with multiple rounds.
Why?
- Time complexity: O(k log³ n) where k is number of rounds
- Accuracy: Error probability < (1/4)^k
- Practical: 20 rounds give certainty > 99.9999999%
Real-world use case:
RSA-2048 encryption uses primes with ~600 digits. Generating these requires:
1. Generate random 600-digit odd number
2. Run Miller-Rabin test with 64 rounds
3. If composite, increment by 2 and repeat
4. Average attempts: ~300 (based on prime density)
For complete implementation with BigInt and RSA key generation, see our Large Prime Number Detection Guide.
Performance Optimization
Making your prime checker blazingly fast.
1. Skip even numbers (except 2):
// Before: Check all numbers
for (let i = 2; i <= n; i++) // Slow
// After: Skip evens
if (n === 2) return true;
if (n % 2 === 0) return false;
for (let i = 3; i <= Math.sqrt(n); i += 2) // 2x faster
2. Use 6k±1 optimization:
All primes > 3 are of form 6k±1. This eliminates 2/3 of candidates.
// Check only numbers of form 6k-1 and 6k+1
for (let i = 5; i * i <= n; i += 6) {
if (n % i === 0 || n % (i + 2) === 0) return false;
}
Performance gain:
- Numbers checked: Reduced by 67%
- Speed improvement: ~3x faster
3. Wheel factorization (advanced):
Pre-eliminate multiples of first k primes (2, 3, 5, 7...).
Example with 2, 3, 5:
Only check: 1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47... (mod 30)
- Eliminates: 77% of candidates
- Implementation: More complex, but 5-10x faster for large n
4. Memoization for repeated checks:
const primeCache = new Map();
function isPrimeCached(n) {
if (primeCache.has(n)) {
return primeCache.get(n);
}
const result = isPrime(n);
primeCache.set(n, result);
return result;
}
When to use:
- Checking same numbers repeatedly
- Finding primes in a range
- Educational applications with common test cases
Trade-off:
- Memory usage increases
- Only beneficial if same numbers checked multiple times
5. Parallel processing (multi-core):
For checking many numbers, distribute work across CPU cores.
JavaScript (Web Workers):
// Main thread
const worker = new Worker('prime-worker.js');
worker.postMessage({start: 1000000, end: 2000000});
// Worker thread (prime-worker.js)
self.onmessage = (e) => {
const {start, end} = e.data;
const primes = findPrimesInRange(start, end);
self.postMessage(primes);
};
Python (multiprocessing):
from multiprocessing import Pool
def find_primes_parallel(start, end, num_processes=4):
pool = Pool(num_processes)
chunk_size = (end - start) // num_processes
ranges = [
(start + i * chunk_size, start + (i + 1) * chunk_size)
for i in range(num_processes)
]
results = pool.starmap(find_primes_in_range, ranges)
pool.close()
pool.join()
return [p for sublist in results for p in sublist]
Speedup:
- Single-core: 1x (baseline)
- Quad-core: ~3.8x faster
- 8-core: ~7.5x faster
- 16-core: ~14x faster
Diminishing returns: Overhead limits perfect scaling.
Common Mistakes to Avoid
Learn from these frequent errors.
Mistake #1: Forgetting edge cases
// ❌ Wrong: Doesn't handle 1, 2, or negative numbers
function isPrimeWrong(n) {
for (let i = 2; i < n; i++) {
if (n % i === 0) return false;
}
return true;
}
isPrimeWrong(1); // Returns true (WRONG!)
isPrimeWrong(2); // Returns true (correct, but inefficient)
isPrimeWrong(-5); // Returns true (WRONG!)
// ✅ Correct: Handle all edge cases
function isPrimeCorrect(n) {
if (n <= 1) return false; // Rejects 0, 1, negatives
if (n === 2) return true; // Optimize for 2
if (n % 2 === 0) return false; // Reject even numbers
for (let i = 3; i <= Math.sqrt(n); i += 2) {
if (n % i === 0) return false;
}
return true;
}
Mistake #2: Inefficient loop bounds
// ❌ Wrong: Checks unnecessary divisors
for (let i = 2; i < n; i++) // Too many checks
// ✅ Correct: Only check up to √n
for (let i = 2; i <= Math.sqrt(n); i++)
Why it matters:
- Checking 1,000,003: Wrong method checks ~1 million numbers, correct checks ~1,000
- Speedup: 1,000x faster
Mistake #3: Integer overflow in large numbers
// ❌ JavaScript: Precision loss above 2^53
const huge = 9007199254740992; // 2^53
console.log(huge + 1 === huge); // true (precision lost!)
// ✅ Use BigInt for large numbers
const hugeBigInt = 9007199254740992n;
console.log(hugeBigInt + 1n === hugeBigInt); // false (correct)
Other languages:
- Java: Use long (2^63-1) or BigInteger for unlimited size
- Python: Automatic arbitrary precision (no overflow issues)
- C: Use long long or GMP library for huge numbers
Mistake #4: Floating-point errors in square root
// ❌ Potential floating-point precision issues
for (let i = 2; i <= Math.sqrt(n); i++)
// ✅ Better: Use integer comparison
for (let i = 2; i * i <= n; i++)
Why it matters:
- Math.sqrt(n) returns floating-point number
- Floating-point comparison can have precision errors
- Integer multiplication i * i is exact and often faster
Mistake #5: Not considering 2 as special case
// ❌ Inefficient: Checks all numbers
for (let i = 2; i <= Math.sqrt(n); i++)
// ✅ Optimized: Skip even numbers (except 2)
if (n === 2) return true;
if (n % 2 === 0) return false;
for (let i = 3; i <= Math.sqrt(n); i += 2) // Only odd numbers
Performance impact:
- Eliminates 50% of iterations
- Nearly 2x faster for large numbers
Prime Number Check Use Cases
Where prime checking matters in real projects.
1. Cryptography (Security)
Application: RSA encryption key generation
import random
def generate_rsa_prime(bits=1024):
"""Generate a probable prime for RSA encryption."""
while True:
# Generate random odd number of specified bit length
candidate = random.getrandbits(bits) | 1
# Quick trial division
if any(candidate % p == 0 for p in [2, 3, 5, 7, 11, 13]):
continue
# Miller-Rabin primality test
if is_prime_miller_rabin(candidate, rounds=64):
return candidate
# Generate 2048-bit RSA key pair
p = generate_rsa_prime(1024)
q = generate_rsa_prime(1024)
n = p * q # Modulus for RSA
Why primes? RSA security relies on the difficulty of factoring n = p × q when p and q are large primes.
2. Hash Table Sizing
Application: Optimizing hash table performance
function getNextPrimeSize(currentSize) {
// When hash table needs resizing, use prime size
let candidate = currentSize * 2 + 1;
while (!isPrime(candidate)) {
candidate += 2; // Check only odd numbers
}
return candidate;
}
class HashTable {
constructor(initialSize = 101) { // Start with prime
this.size = initialSize;
this.table = new Array(this.size);
}
resize() {
const newSize = getNextPrimeSize(this.size);
// ... rehashing logic
}
}
Why primes? Prime-sized tables reduce clustering and collisions in hash functions.
3. Pseudorandom Number Generation
Application: Linear Congruential Generator (LCG)
// LCG parameters (must use prime modulus for full period)
#define PRIME_MODULUS 2147483647 // 2^31 - 1 (Mersenne prime)
#define MULTIPLIER 48271
#define INCREMENT 0
unsigned long long seed = 12345;
unsigned long random_next() {
seed = (MULTIPLIER * seed + INCREMENT) % PRIME_MODULUS;
return seed;
}
Why primes? Prime modulus ensures maximum period length in LCGs.
4. Competitive Programming
Application: Prime counting in range (common interview question)
def count_primes(n):
"""Count primes less than n using Sieve of Eratosthenes."""
if n < 2:
return 0
is_prime = [True] * n
is_prime[0] = is_prime[1] = False
for i in range(2, int(n ** 0.5) + 1):
if is_prime[i]:
for j in range(i * i, n, i):
is_prime[j] = False
return sum(is_prime)
# Example: How many primes less than 1 million?
print(count_primes(1000000)) # Output: 78,498
Common interview problems:
- Count primes in range [L, R]
- Find nth prime number
- Goldbach conjecture verification
- Twin prime detection
5. Mathematical Research
Application: Searching for Mersenne primes (2^p - 1)
def is_mersenne_prime(p):
"""Check if 2^p - 1 is prime (Lucas-Lehmer test)."""
if p == 2:
return True
# Lucas-Lehmer sequence
s = 4
M = (1 << p) - 1 # 2^p - 1
for _ in range(p - 2):
s = (s * s - 2) % M
return s == 0
# Known Mersenne primes
mersenne_primes = [2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127]
for p in mersenne_primes:
Mp = (1 << p) - 1
print(f"2^{p} - 1 = {Mp} is {'prime' if is_mersenne_prime(p) else 'composite'}")
Real impact: As of 2024, the largest known prime is 2^82,589,933 - 1 (24,862,048 digits), discovered by GIMPS project.
FAQ: Common Prime Number Questions
Q1: What is the fastest way to check if a number is prime?
Answer: It depends on the number size and your use case.
For small numbers (< 10,000):
Use simple trial division up to √n. It's fast enough and easy to implement.
For medium numbers (10,000 - 10^12):
Use optimized trial division with 6k±1 optimization.
For large numbers (> 10^12):
Use Miller-Rabin probabilistic test with 20-64 rounds. For numbers with 100+ digits, this is the only practical method.
For finding all primes in a range:
Use Sieve of Eratosthenes if you have enough memory.
Instant solution: Use Tool Master Prime Checker for numbers up to 2^53-1 with instant results.
Q2: Is 1 a prime number?
Answer: No, 1 is not a prime number.
Mathematical definition: A prime must have exactly two distinct divisors: 1 and itself.
Why 1 doesn't qualify:
- 1 has only one divisor (itself)
- Including 1 as prime would break fundamental theorem of arithmetic
- Every number would have infinite prime factorizations (e.g., 6 = 2 × 3 = 1 × 2 × 3 = 1 × 1 × 2 × 3...)
Historical note: Mathematicians once considered 1 prime, but modern mathematics excludes it for theoretical consistency.
Q3: What is the largest known prime number?
Answer: As of December 2024, the largest known prime is:
2^82,589,933 - 1
Key facts:
- Digits: 24,862,048 digits
- Discovery date: December 7, 2018
- Discovered by: Patrick Laroche (GIMPS project)
- Type: Mersenne prime (form 2^p - 1)
- Prize: Won $3,000 GIMPS award
Context:
- If printed in 12-point font, it would fill ~9,000 pages
- Took an Intel i5-4590T processor 12 days to verify
- Only 51 Mersenne primes are known
Next target: GIMPS is searching for the first 100-million-digit prime (with $150,000 prize).
Q4: How many prime numbers are there?
Answer: There are infinitely many prime numbers.
Euclid's proof (300 BCE):
Assume there are finitely many primes: p₁, p₂, ..., pₙ.
Consider N = (p₁ × p₂ × ... × pₙ) + 1.
N is not divisible by any prime p₁, p₂, ..., pₙ (remainder 1).
Therefore, N is either prime itself, or divisible by a prime not in our list.
Contradiction! The list cannot be finite.
Prime density:
- Primes become less frequent as numbers grow larger
- Approximately n/ln(n) primes less than n
- Between 1-100: 25 primes
- Between 1-1,000: 168 primes
- Between 1-1,000,000: 78,498 primes
Q5: Can even numbers be prime?
Answer: Only one even number is prime: 2.
Why 2 is special:
- 2 is the smallest and only even prime
- All other even numbers are divisible by 2, so they're composite
Key insight:
This is why prime-checking algorithms skip even numbers after checking 2:
if (n === 2) return true;
if (n % 2 === 0) return false; // All other evens are composite
Interesting fact: This makes 2 the "oddest" prime number (pun intended).
Q6: What's the difference between prime and coprime?
Answer: These are completely different concepts.
Prime number:
- Has exactly two divisors: 1 and itself
- Examples: 2, 3, 5, 7, 11, 13
- Property of a single number
Coprime (relatively prime):
- Two numbers whose greatest common divisor (GCD) is 1
- Examples: (8, 15), (14, 25), (9, 16)
- Property of a pair of numbers
Key difference:
8 is NOT prime (8 = 2 × 2 × 2)
15 is NOT prime (15 = 3 × 5)
But 8 and 15 ARE coprime (GCD(8, 15) = 1, no common factors)
Check coprimality: Use GCD & LCM Calculator to find if two numbers are coprime.
Q7: How do I check if a number is prime in Excel?
Answer: Excel doesn't have a built-in ISPRIME function, but you can create a formula.
Simple formula (works for small numbers):
=IF(A1<=1, FALSE, IF(A1=2, TRUE, IF(MOD(A1,2)=0, FALSE,
SUMPRODUCT(--(MOD(A1,ROW(INDIRECT("3:"&INT(SQRT(A1))&":2")))=0))=0)))
Put the number to check in cell A1.
Limitation: Slow for numbers > 10,000.
Better solution: Use Tool Master Prime Checker:
1. Enter your number
2. Get instant result
3. Copy result back to Excel if needed
For frequent Excel use: Create a custom VBA function (macro) for better performance.
Q8: What is a twin prime?
Answer: Twin primes are pairs of primes that differ by 2.
Examples:
- (3, 5)
- (5, 7)
- (11, 13)
- (17, 19)
- (29, 31)
- (41, 43)
- (71, 73)
Twin Prime Conjecture:
Are there infinitely many twin primes?
Status: Unproven! This is one of the oldest open problems in mathematics.
Recent progress:
- 2013: Yitang Zhang proved gaps of at most 70 million exist infinitely often
- Polymath project reduced gap to 246
- Complete proof for gap of 2 remains elusive
Largest known twin primes: 2,996,863,034,895 × 2^1,290,000 ± 1 (388,342 digits each)
Q9: How are prime numbers used in cryptography?
Answer: Primes are fundamental to modern encryption, especially RSA.
RSA encryption basics:
- Key generation:
- Choose two large primes p and q (typically 1024 bits each)
- Compute n = p × q (this becomes your public modulus)
- Public key: (n, e) where e is usually 65537
-
Private key: (n, d) where d is computed from p, q, and e
-
Encryption:
-
Message M is encrypted as C = M^e mod n
-
Decryption:
- Ciphertext C is decrypted as M = C^d mod n
Why it's secure:
- Easy to multiply two primes: p × q = n (milliseconds)
- Hard to factor n back to p and q (would take millions of years for 2048-bit numbers)
- Security relies on prime factorization being computationally difficult
Real-world use:
- HTTPS websites
- Digital signatures
- Cryptocurrency wallets
- Secure messaging apps
Fun fact: Breaking RSA-2048 encryption would require more computational power than exists on Earth.
Q10: Can I check prime numbers offline?
Answer: Absolutely! Multiple options exist.
Option 1: Tool Master Prime Checker (recommended)
- Visit Tool Master Prime Checker once
- Bookmark the page
- Works completely offline in your browser
- No installation needed
- 100% private (all calculations local)
How it works:
1. The tool loads JavaScript code to your browser
2. All prime checking runs locally on your device
3. No internet connection needed after initial load
4. Your numbers never leave your computer
Test it: Load the page, then disconnect internet and check a prime. It still works!
Option 2: Install a programming language
- Python, Java, JavaScript (Node.js), or C
- Use the code examples from this guide
- Create your own command-line tool
Option 3: Calculator apps
- Some scientific calculator apps include prime checking
- Usually limited to smaller numbers
Option 4: Spreadsheet formulas
- Excel or Google Sheets formulas
- Slower but works for simple cases
Best for most users: Tool Master Prime Checker combines ease of use, speed, privacy, and offline capability.
Image 3: Student using prime checker on laptop for math homework
Scene Description:
A female Asian high school student sits at a wooden desk in a cozy home study area, working on math homework. Her laptop displays the Tool Master Prime Checker interface with a large number entered and the result showing "PRIME" in green text. Scattered on the desk are a spiral-bound math textbook open to a page about number theory, handwritten notes with prime number sequences, a scientific calculator, and a pencil. Soft afternoon sunlight streams through a nearby window, illuminating her focused expression. A small desk lamp provides additional warm lighting. In the blurred background, a bookshelf with textbooks is visible.
Visual Focus:
- Foreground: Laptop screen showing prime checker result (40% of frame), textbook and notes (30%)
- Mid-ground: Student's concentrated face, natural studying posture
- Background: Warm, inviting study environment with soft focus
Must-Appear Elements:
- Tool Master Prime Checker interface clearly visible on laptop
- "PRIME" result displayed prominently in green
- Handwritten math notes with numbers visible
- Scientific calculator
- Math textbook with "Number Theory" or similar visible
Chinese Text to Display:
None
Image/Character Style:
- Realistic photography style, natural indoor lighting
- Asian female student (16-18 years old), wearing casual study clothes
- Authentic studying environment
- Natural expressions of concentration and learning
Color Palette:
Warm, educational, inviting, natural afternoon light, green accent for prime result
Avoid Elements:
Light bulbs, gears, abstract symbols, floating numbers, magic effects
Slug:
student-using-prime-checker-homework-laptop
Conclusion: Mastering Prime Number Checking in 2025
You now have everything you need to check prime numbers efficiently.
Key Takeaways
For quick checks:
- Use Tool Master Prime Checker for instant, private results
- Bookmark it for homework, coding, or research
- 100% free, works offline, no registration needed
For programming:
- Python: Best for learning and flexibility
- Java: Best for enterprise applications
- JavaScript: Best for web tools and education
- C: Best for maximum performance
For large numbers:
- Use Miller-Rabin algorithm
- Consider GMP library or BigInt types
- Cryptographic applications require specialized approaches
For understanding:
- All primes > 3 follow form 6k±1
- Only check divisors up to √n
- 2 is the only even prime
Next Steps
Want to deepen your knowledge?
Choose your path:
- Learn Python prime checking → Python Prime Number Tutorial
- Master Java implementations → Java Prime Best Practices
- Explore advanced algorithms → Prime Algorithms Comparison
- Build your own tool → JavaScript Advanced Guide
- Understand cryptography → Large Prime Detection
- Quick learning → Learn Prime Checking in 10 Minutes
For developers:
Want to see how Tool Master Prime Checker is built? Check the technical implementation documentation with complete source code walkthrough.
Explore more math tools:
Browse all Math Tools including factorial calculator, GCD/LCM finder, and prime factorization.
💡 Final Reminder
Tool Master provides 33 free tools across 8 categories—all running locally in your browser for maximum privacy.
No registration, no data collection, no hidden fees.
Bookmark Tool Master for instant access to professional-grade tools whenever you need them.
If this guide helped you, share it with classmates, colleagues, or anyone learning about prime numbers!
References
- Crandall, R., & Pomerance, C. (2005). Prime Numbers: A Computational Perspective. Springer.
- Rosen, K. H. (2019). Elementary Number Theory and Its Applications (7th ed.). Pearson.
- Agrawal, M., Kayal, N., & Saxena, N. (2004). "PRIMES is in P." Annals of Mathematics, 160(2), 781-793.
- Rabin, M. O. (1980). "Probabilistic algorithm for testing primality." Journal of Number Theory, 12(1), 128-138.
- GIMPS - Great Internet Mersenne Prime Search. (2024). Latest Mersenne Prime Discoveries. mersenne.org
- NIST. (2023). FIPS 186-5: Digital Signature Standard (DSS). National Institute of Standards and Technology.
- Atkin, A. O. L., & Bernstein, D. J. (2004). "Prime sieves using binary quadratic forms." Mathematics of Computation, 73(246), 1023-1030.