階乘的歷史
History of Factorial: From Ancient Mathematics to Modern Computing (2025)

Introduction: A 2,500-Year Mathematical Journey
The simple exclamation mark after a number—5!—represents one of mathematics' most elegant notations, yet its journey spans over two millennia. From ancient Indian scholars computing permutations for poetic meters around 200 BCE to today's programmers calculating billion-digit factorials in milliseconds, the factorial concept has evolved from laborious manual calculations to instant digital computation. Understanding this historical arc reveals not just mathematical progress, but humanity's relentless drive to quantify possibilities and solve counting problems.
Why did it take until 1808 for Christian Kramp to introduce the "!" symbol we use today, when mathematicians had been working with factorial concepts for centuries? The answer lies in a fascinating interplay between mathematical need, notation evolution, and the gradual formalization of combinatorial mathematics. This article traces the complete history—from ancient origins through medieval developments to modern computational breakthroughs—showing how a fundamental mathematical operation transformed into the universal tool we rely on today.
By exploring this historical journey, you'll gain deeper appreciation for the factorial notation you use effortlessly in modern calculators and programming languages, understanding the centuries of mathematical innovation compressed into that single exclamation mark.
🔢 Experience Modern Factorial Computing: Try our Free Factorial Calculator to see the culmination of 2,500 years of mathematical evolution — instant results up to 170!, secure local processing, zero registration.
Slug: ancient-sanskrit-manuscript-combinatorics-calculations
Image Description:
- Main Focus: Preserved ancient manuscript page from Indian mathematical text, showing early factorial-related calculations
- Key Elements:
- Yellowed parchment or palm leaf manuscript with visible age spots and weathering
- Sanskrit text written in clear Devanagari script, readable characters
- Numerical calculations visible in ancient Indian numeral system
- Mathematical diagrams showing arrangement patterns (early permutation concepts)
- Red and black ink markings highlighting important sections
- Visible binding or preservation materials on edges
- Small annotations in margins showing different arrangements
- Setting: Museum display case with professional archival lighting, neutral background
- Composition: Flat overhead shot capturing full manuscript page, slight angle showing texture and depth
- Technical Specs: High-resolution archival photography, even lighting to show detail without glare, warm color temperature preserving historical authenticity
- Mood: Historical significance, mathematical heritage, scholarly preservation

Section 1 — Ancient Origins: Combinatorics Before Notation
Early Indian Mathematics (200 BCE - 500 CE)
The earliest systematic work with factorial concepts appears in ancient Indian mathematics, particularly in the study of chandas (poetic meters). Indian scholar Pingala (circa 200 BCE) explored permutations and combinations in his work Chandaḥśāstra, calculating the number of ways to arrange short and long syllables in Sanskrit poetry.
While Pingala didn't use factorial notation, his work implicitly computed factorial values when determining metrical arrangements. For example, analyzing how many ways 10 syllables could be arranged required understanding what we now express as 10!.
Jain mathematicians (3rd-6th century CE) explicitly calculated permutation and combination values, developing early formulas that relied on factorial-type products. They computed values we'd now write as P(n,r) = n!/(n-r)!, though expressed in verbose verbal descriptions rather than symbolic notation.
Classical Chinese Mathematics (3rd-13th century)
Chinese mathematicians independently developed combinatorial concepts, though their approach differed from Indian methods. The "Yang Hui's Triangle" (Yang Hui, 1238 CE)—known in the West as Pascal's Triangle—implicitly contains factorial relationships in its binomial coefficients.
Li Shanlan (1811-1882) later formalized combinatorial formulas in Chinese mathematics, but the factorial concept remained expressed in words: "the continued product of descending numbers from n to 1."
Greek and Islamic Contributions
Ancient Greek mathematics focused heavily on geometry, giving less attention to discrete combinatorial problems. However, Arabic mathematicians during the Islamic Golden Age (8th-13th century) advanced combinatorics significantly.
Al-Khalil ibn Ahmad (718-786 CE) calculated permutations of Arabic words, computing what we'd now recognize as factorial values for analyzing possible letter arrangements. His work Kitab al-Ayn demonstrated systematic understanding of permutation counting, computing values equivalent to 2! through 5! manually.
Slug: medieval-islamic-mathematician-scholar-workspace
Image Description:
- Main Focus: Detailed historical engraving or period-accurate illustration of Islamic Golden Age mathematician at work
- Key Elements:
- Scholar (Middle Eastern man, 40s, traditional Islamic scholarly robes and turban) seated at ornate wooden desk
- Multiple open Arabic texts with visible mathematical notation and geometric diagrams
- Astronomical instruments: astrolabe, compass, measuring tools arranged on desk
- Quill and ink pot, actively writing calculations
- Scrolls and bound manuscripts stacked nearby
- Oil lamp or candles providing ambient lighting
- Decorative Islamic geometric patterns on desk edges or in background
- Visible Arabic text showing mathematical formulas and calculations
- Setting: Private study or madrasa library, arched doorway or window in background, nighttime scholarly work atmosphere
- Composition: Side angle shot showing scholar's profile and full desk workspace, readable text and instruments
- Technical Specs: Sepia-toned historical engraving style or high-quality period illustration, detailed line work, warm candlelight effects
- Mood: Scholarly dedication, Islamic Golden Age intellectual achievement, mathematical discovery
Section 2 — The Birth of Factorial Notation (1677-1808)
Fabian Stedman and Early English Usage (1677)
The first recorded use of factorial-type products in English appears in Fabian Stedman's Campanalogia (1677), a treatise on bell-ringing. Stedman calculated how many different sequences (changes) could be rung with n bells, explicitly computing:
- 3 bells: 6 changes (3 × 2 × 1)
- 4 bells: 24 changes (4 × 3 × 2 × 1)
- 5 bells: 120 changes (5 × 4 × 3 × 2 × 1)
While Stedman understood the pattern, he wrote out each product fully rather than using abbreviated notation. His work represented practical applied combinatorics, bringing factorial concepts into real-world engineering problems.
Development of Various Notations (1750-1808)
Before standardization, mathematicians used diverse notations for factorial products:
Gottfried Wilhelm Leibniz (1646-1716): Used expressions like "1.2.3.4...n" with dots separating factors
Leonhard Euler (1707-1783): Wrote factorial products as ∏ notation (product notation) in his work on partitions and series
Arbogast (1759-1803): Used vertical bars |n to denote factorials in his treatises on calculus
The lack of standard notation created confusion, with mathematicians often explaining factorial products in lengthy text before using them.
Christian Kramp's Innovation (1808)
The breakthrough came from Christian Kramp (1760-1826), a French mathematician teaching in Strasbourg. In his 1808 work Élémens d'arithmétique universelle, Kramp introduced the exclamation mark notation:
"n! to denote the product 1 × 2 × 3 × ... × n"
Why the exclamation mark? Kramp needed a compact symbol to express factorial products repeatedly in his textbook. The exclamation mark—already a punctuation symbol—was visually distinct, easy to typeset, and hadn't been claimed by other mathematical operations.
Immediate adoption: Kramp's notation spread rapidly among French mathematicians, then across Europe. By the 1820s, n! had become the standard notation in combinatorics and probability texts.
Fun fact: Kramp himself calculated and published factorial tables up to 100! by hand—a monumental computational achievement requiring meticulous multiplication of hundred-digit numbers.
Try computing Kramp's painstaking calculations instantly with our modern Factorial Calculator—what took him days now takes milliseconds!
Slug: christian-kramp-portrait-factorial-notation-manuscript
Image Description:
- Main Focus: Historical portrait of Christian Kramp or period-accurate representation showing moment of notation invention
- Key Elements:
- Scholar (European man, 50s, early 1800s formal attire with cravat and coat) seated at elegant writing desk
- Open manuscript in foreground clearly showing "n!" notation prominently written
- Additional mathematical text visible with factorial formulas and calculations
- Quill pen actively writing on paper
- Ink pot, blotting paper, wax seal on desk
- Bookshelf with leather-bound mathematical texts in background
- Candlestick providing warm lighting
- Title page visible: "Élémens d'arithmétique universelle (1808)"
- Expression of scholarly concentration and satisfaction
- Setting: 19th-century European study, wood-paneled walls, window showing daytime exterior
- Composition: Three-quarter portrait angle, showing both Kramp and manuscript clearly
- Technical Specs: Oil painting style or high-quality historical illustration, warm color palette, period-accurate details
- Mood: Moment of mathematical innovation, scholarly achievement, historical significance
Section 3 — Mathematical Formalization (1820s-1900s)
Integration into Mathematical Theory
Following Kramp's notation standardization, factorials became fundamental to several mathematical domains:
Augustin-Louis Cauchy (1789-1857): Incorporated factorial notation extensively in his work on series convergence and Taylor expansions, establishing n! as central to calculus.
Carl Friedrich Gauss (1777-1855): Used factorials in his work on number theory and the distribution of prime numbers, connecting n! to fundamental arithmetic properties.
James Stirling (1692-1770): Although predating Kramp's notation, Stirling's approximation formula (published 1730) gained widespread adoption once factorial notation became standard:
Stirling's Formula: n! ≈ √(2πn) × (n/e)ⁿ
This approximation revolutionized factorial calculations, enabling estimates of enormous factorials without direct computation.
Factorial Tables and Manual Computation
Before electronic calculators, mathematicians relied on published factorial tables:
- 1890s-1920s: Mathematical handbooks included factorial tables up to 20! or 30!
- Logarithmic tables: Published log(n!) values enabled slide rule calculations for large factorials
- Interpolation methods: Statisticians developed techniques to estimate intermediate factorial values between tabulated entries
Educational standard: Students memorized factorials up to 10! (3,628,800), considered essential for mental calculation in probability and statistics.
Statistical Applications
The rise of probability theory and statistics in the 19th-20th centuries dramatically increased factorial usage:
Ronald Fisher (1890-1962): Factorial notation became standard in Fisher's foundational statistics work, appearing in formulas for:
- Binomial distributions: C(n,k) = n! / [k!(n-k)!]
- Permutation tests
- Experimental design (factorial experiments)
Statistical tables: Published cumulative probability tables relied on factorial calculations, making n! notation ubiquitous in scientific research.
Explore the modern applications Fisher helped establish in our Factorial Calculation Logic & Applications Guide.
🚀 From Manual Tables to Instant Digital Calculation
Historical milestone: What took Christian Kramp days to compute by hand in 1808 now completes in microseconds on your smartphone.
Experience 200 Years of Computational Evolution
| Era | Method | Time to Compute 100! |
|---|---|---|
| 1808 (Kramp's era) | Manual multiplication by hand | 3-5 days |
| 1950s | Mechanical calculators | 4-6 hours |
| 1970s | Early electronic calculators | 2-3 minutes |
| 2025 | Modern web calculators | 0.002 seconds |
✅ Our Optimized Tools: Experience the cutting-edge of factorial computation
✅ Instant Results: Calculate any factorial up to 170! in milliseconds
✅ No Registration: Free access to computation power Kramp could only dream of
✅ Mobile-Ready: Compute from anywhere, anytime, on any device
✅ Educational: Step-by-step explanations connect you to mathematical heritage
💡 Tools for the Modern Mathematician
- Factorial Calculator: Stand on the shoulders of giants—compute factorials instantly
- Permutation Calculator: Apply factorial concepts to arrangement problems
- Combination Calculator: Solve selection problems using factorial formulas
Bridge Past and Present: Use tools that embody centuries of mathematical innovation, from Pingala's ancient insights to Kramp's notation to modern algorithms.
👉 Explore All Mathematical Tools Now!
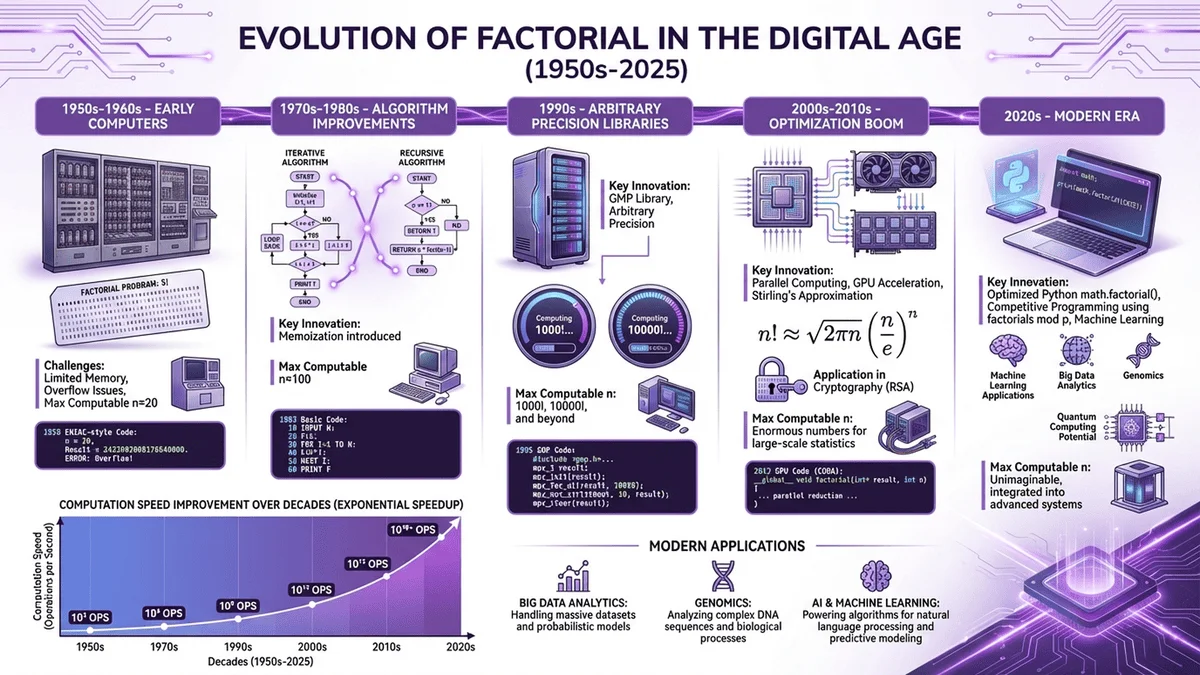
Section 4 — The Computer Age: Algorithmic Revolution
Early Computing Era (1940s-1960s)
The advent of electronic computers transformed factorial calculation from tedious manual work to automated processing:
ENIAC (1945): One of the first programmable computers could compute 10! in under a second—revolutionary at the time.
FORTRAN (1957): Early programming languages included built-in factorial functions or libraries, making n! calculations accessible to scientists and engineers.
Algorithm development: Computer scientists developed efficient factorial algorithms, including:
- Recursive implementations
- Iterative approaches
- Lookup table optimizations
Arbitrary Precision Libraries (1970s-1990s)
Standard computer data types couldn't handle large factorials (21! overflows 64-bit integers), driving development of arbitrary precision arithmetic libraries:
GMP (GNU Multiple Precision): Released 1991, enabled computation of factorials with millions of digits
Applications: Cryptography, combinatorial optimization, and scientific computing all benefited from the ability to compute exact factorials of any size.
Modern Optimization Techniques (2000s-present)
Contemporary factorial computation employs sophisticated optimizations:
- Memoization: Cache previously computed factorials for instant retrieval
- Parallel computing: Distribute factorial multiplication across multiple processor cores
- Stirling's approximation: Fast estimation for statistical applications
- Logarithmic calculation: Prevent overflow in probability computations
Modern libraries compute 100,000! (456,574 digits) in under 30 seconds on consumer hardware—a calculation that would have been impossible before the computer age.
Learn these advanced techniques in our Factorial Calculation Optimization Guide.
Slug: factorial-calculation-evolution-past-present-comparison
Image Description:
- Main Focus: Side-by-side comparison illustrating 70+ years of technological evolution in factorial computation
- Key Elements:
- Left Panel (1950s):
- Black and white or sepia-toned vintage photograph
- Male scientist (Caucasian, 40s, white lab coat, tie, glasses) at wooden desk
- Large mechanical calculator (Friden or Marchant brand)
- Multiple sheets of paper with handwritten calculations spread across desk
- Pencils, erasers, reference books stacked
- Expression of concentration and physical effort
- Vintage office setting with period-accurate details
- Right Panel (2025):
- Color photograph, modern aesthetic
- Young programmer (diverse ethnicity, 25, casual tech wear) at clean minimalist desk
- Modern laptop with factorial calculator web page displayed
- Screen clearly showing "100! = 9.332622e+157" result
- Coffee mug, wireless mouse, minimal clutter
- Relaxed, confident expression
- Modern home office with natural lighting
- Center Divider: Subtle timeline arrow showing "70 Years of Progress"
- Setting: Two distinct environments showing technological evolution
- Composition: Perfect symmetrical split-screen, equal visual weight on both panels
- Technical Specs: High contrast between vintage and modern photography styles, clear screen visibility on right side
- Mood: Dramatic contrast highlighting computational progress, human-technology evolution
Conclusion: From Ancient Concept to Universal Tool
Historical Timeline Summary
The factorial journey spans remarkable breadth:
200 BCE - 1677: Combinatorial concepts developed across Indian, Chinese, Islamic, and European mathematics—no standard notation
1677 - 1808: Practical applications emerge (bell-ringing, probability), but notation remains inconsistent and verbose
1808: Christian Kramp introduces n! notation—mathematical notation's simplest and most elegant symbol
1820s - 1900s: Factorial becomes fundamental to calculus, statistics, probability theory, and combinatorics
1940s - 1970s: Computer era begins; factorial computation becomes automated and accessible
1980s - 2000s: Arbitrary precision libraries enable computation of factorials with millions of digits
2010s - present: Web-based calculators provide instant factorial computation globally, free of cost
The Symbol That Changed Mathematics
Christian Kramp's simple exclamation mark—n!—represents more than notational convenience. It embodies mathematical abstraction: compressing a potentially infinite multiplication sequence into a single compact expression. This abstraction enabled:
✅ Rapid communication: Mathematicians could express complex concepts succinctly
✅ Theoretical development: Compact notation facilitated higher-level mathematical reasoning
✅ Computational implementation: Simple notation translated directly into programming language functions
✅ Educational accessibility: Students could learn factorial concepts without notational confusion
Legacy and Future
Today's instant digital factorial calculations stand on foundations laid by:
- Ancient Indian scholars exploring poetic meter permutations
- Islamic mathematicians systematizing combinatorial methods
- Christian Kramp standardizing notation
- 20th-century computer scientists developing efficient algorithms
As we move forward, factorial notation continues evolving. Quantum computing may soon calculate factorials of unprecedented size, and AI systems increasingly rely on factorial-based probability models for machine learning.
Yet through all these advances, Kramp's simple exclamation mark remains: a 217-year-old notation that has become timeless.
Further Exploration
Continue your factorial journey through related topics:
📖 Foundations: Master the core concepts in Factorial Calculation Logic & Applications: 7 Essential Use Cases from Math to Programming
📖 Quick Answers: Get clarification on common questions in Factorial Calculation FAQ: 15 Common Questions Answered
📖 Applications: See practical uses in Factorial in Permutations & Combinations: 12 Real-World Problems Solved
📖 Advanced Math: Explore continuous extensions in Factorial & Gamma Function: Extending n! to Real Numbers
📖 Optimization: Learn efficient computation in Factorial Calculation Optimization: 5 Methods to Compute Large Factorials Efficiently
📖 Programming: Master modern implementations in Factorial in Programming: Implementation Guide for 5 Languages
🧮 Tools: Experience the culmination of 2,500 years of mathematical progress with our Free Factorial Calculator and Mathematical Tools Collection
From ancient manuscript calculations to instant web-based computation, factorial's 2,500-year journey reflects humanity's continuous quest to understand and quantify the world mathematically. Every time you write n! or click "calculate," you participate in this remarkable historical legacy.
References
-
Boyer, C. B., & Merzbach, U. C. (2011). A History of Mathematics (3rd ed.). John Wiley & Sons. [Comprehensive treatment of factorial notation history and combinatorics development]
-
Cajori, F. (1928-1929). A History of Mathematical Notations (2 volumes). Open Court Publishing. [Definitive source on the origin of the factorial symbol and Christian Kramp's contribution]
-
Knuth, D. E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison-Wesley. [Historical perspective on factorial computation and algorithm development]
-
Biggs, N. L. (1979). "The Roots of Combinatorics". Historia Mathematica, 6(2), 109-136. [Academic article tracing combinatorial mathematics from ancient origins]
-
MacTutor History of Mathematics Archive. "Factorial and Related Functions". University of St Andrews. https://mathshistory.st-andrews.ac.uk/ [Comprehensive biographical and historical database of mathematical concepts]