階乘、排列與組合問題指南
Factorial in Permutations & Combinations: 12 Real-World Problems Solved (2025 Guide)
Introduction: The Essential Role of Factorials in Combinatorics
Planning a wedding with 5 VIP guests at the head table? You're facing 120 different seating arrangements (5! = 120). Whether you're organizing events, calculating lottery odds, or solving password security problems, factorial calculations are the mathematical backbone of permutations and combinations. In this comprehensive guide, we'll solve 12 real-world problems that demonstrate why factorials are indispensable in combinatorial mathematics.
Understanding the difference between permutations (where order matters) and combinations (where order doesn't matter) is crucial for solving counting problems correctly. We'll explore both concepts through practical examples, provide you with powerful formulas, and show you how to avoid common mistakes that trip up even experienced problem-solvers.
By the end of this guide, you'll confidently tackle everything from team selection problems to circular arrangement puzzles, armed with both theoretical knowledge and practical calculation tools.
🎯 Skip the Manual Math: Use our Free Permutation & Combination Calculator — Instant P(n,r) and C(n,r) calculations with step-by-step explanations, 100% local processing, free forever.
Slug: wedding-seating-arrangement-permutation-chart
Image Description:
- Main Focus: Professional wedding planner (Asian woman, 30s, business attire) sitting with bride and groom at elegant round table
- Key Elements:
- Open laptop screen showing "5 Guests = 120 Arrangements" with visual seating chart diagrams
- Physical seating chart papers spread on table with guest names in different positions
- Bride in white dress and groom in suit examining arrangements
- Crystal chandelier visible in blurred elegant venue background
- Setting: Upscale wedding venue consultation room, large windows with soft natural light
- Composition: Medium shot from 45-degree angle, laptop screen clearly visible on left, couple and planner interacting on right
- Technical Specs: Professional DSLR photography style, sharp focus on laptop and papers, soft bokeh background, warm color temperature 5500K
- Mood: Collaborative, organized, problem-solving atmosphere with elegant wedding planning ambiance
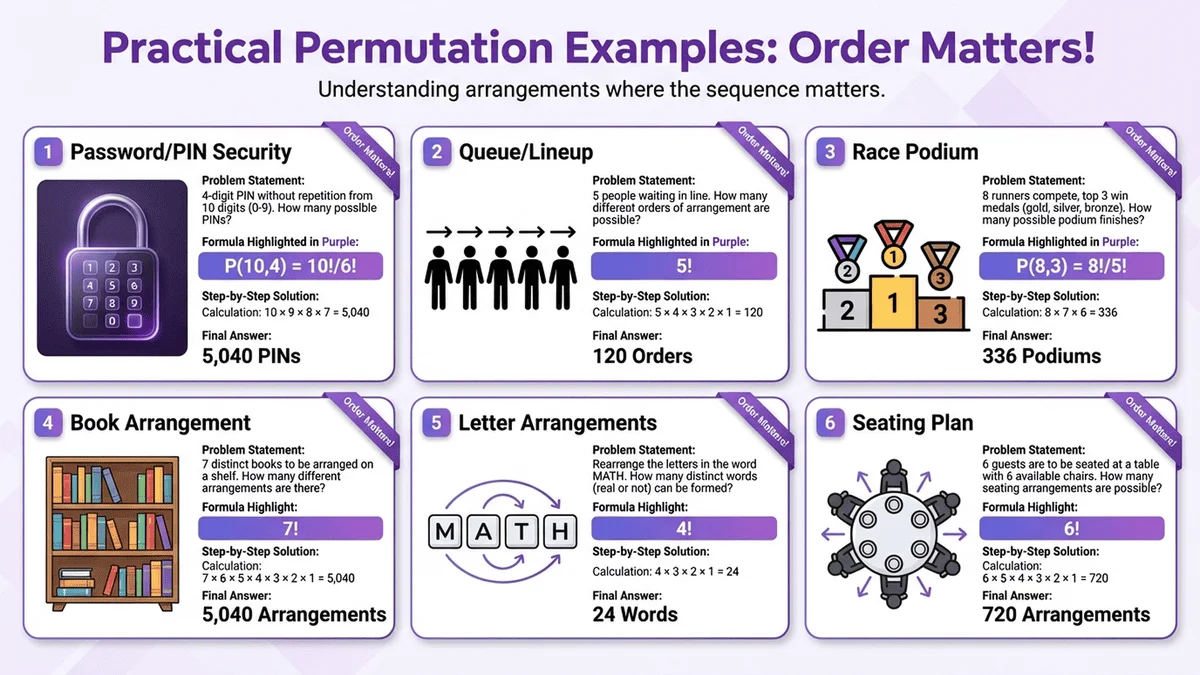
Section 1 — Permutations: When Order Matters
What Are Permutations?
A permutation is an arrangement of objects where the order of selection matters. If you're assigning positions, ranks, or sequences, you're dealing with permutations.
Key characteristic: Changing the order creates a different permutation.
For example: Arranging books on a shelf, assigning race positions, or creating passwords where ABC ≠ BAC.
The Permutation Formula: P(n,r) = n!/(n-r)!
When selecting r items from n total items where order matters:
P(n,r) = n! / (n-r)!
Where:
- n = total number of items available
- r = number of items being selected
- P(n,r) = number of possible permutations
Special case: When selecting all items (r = n), then P(n,n) = n! because (n-n)! = 0! = 1.
Problem 1: Password Permutation Challenge
Question: How many 4-digit passwords can you create using the digits 1, 2, 3, 4, 5 without repetition?
Solution:
- n = 5 (total digits available)
- r = 4 (password length)
- P(5,4) = 5! / (5-4)! = 5! / 1! = 120 / 1 = 120 passwords
Explanation: The first position has 5 choices, second has 4 remaining, third has 3, fourth has 2. Total: 5 × 4 × 3 × 2 = 120.
Try solving this yourself with our Factorial Calculator to verify 5! = 120.
Problem 2: Race Podium Positions
Question: In a race with 8 runners, how many different ways can gold, silver, and bronze medals be awarded?
Solution:
- n = 8 (total runners)
- r = 3 (medal positions)
- P(8,3) = 8! / (8-3)! = 8! / 5! = 40,320 / 120 = 336 ways
Explanation: 8 choices for gold, 7 for silver, 6 for bronze: 8 × 7 × 6 = 336.
Problem 3: Meeting Agenda Order
Question: A committee must discuss 6 different topics. How many different agenda sequences are possible?
Solution:
- n = 6 (total topics)
- r = 6 (all topics must be discussed)
- P(6,6) = 6! = 720 sequences
Explanation: First topic: 6 choices, second: 5 choices, continuing until all are arranged.
Slug: permutation-formula-whiteboard-presentation
Image Description:
- Main Focus: Professional Asian man (35, business casual, standing) presenting permutation concepts at large whiteboard
- Key Elements:
- Whiteboard clearly shows "P(n,r) = n! / (n-r)!" formula in red marker
- Colorful diagram: 8 stick figure runners numbered 1-8 at top
- Three podium boxes labeled "Gold", "Silver", "Bronze" below
- Arrows and calculations showing "8 × 7 × 6 = 336" in blue
- Presenter holding marker, pointing to formula
- Setting: Modern corporate conference room, natural window light, glass walls in background
- Composition: Wide shot capturing full whiteboard and presenter, camera at eye level
- Technical Specs: Sharp focus on whiteboard text and diagrams, professional office lighting, neutral color balance
- Mood: Educational, professional training atmosphere with clear visual teaching
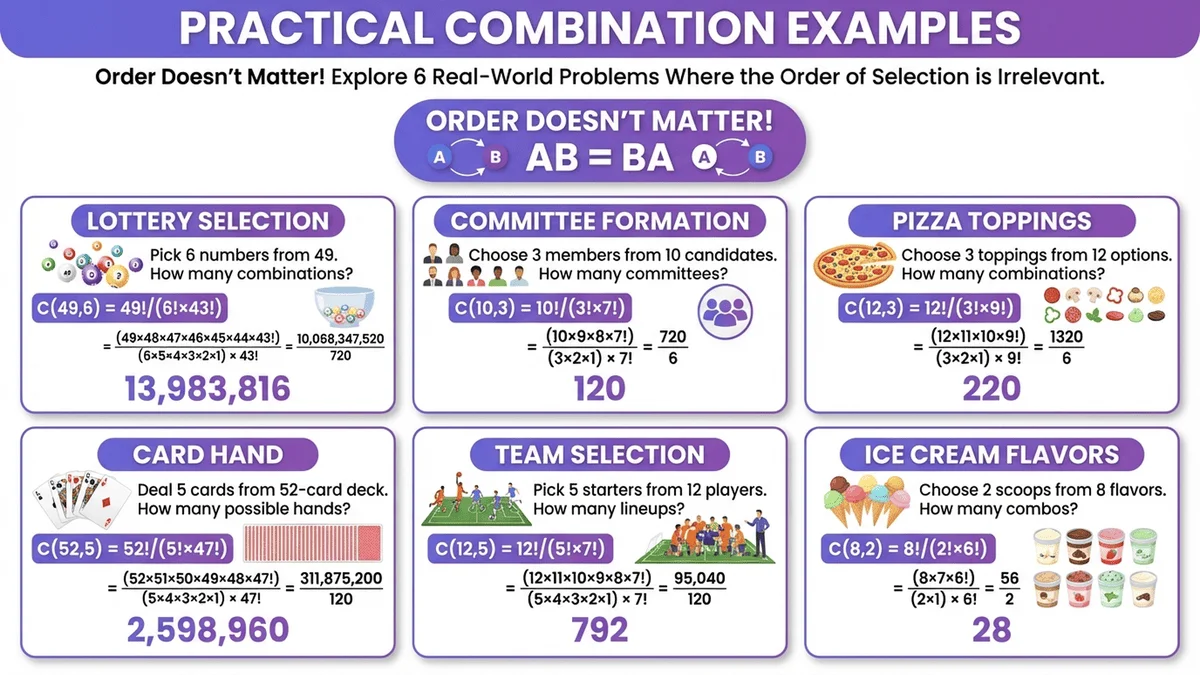
Section 2 — Combinations: When Order Doesn't Matter
What Are Combinations?
A combination is a selection of objects where the order doesn't matter. If you're choosing team members, selecting items, or picking lottery numbers, order is irrelevant.
Key characteristic: ABC and BAC are considered the same combination.
For example: Selecting committee members, choosing pizza toppings, or forming teams where roles aren't assigned.
The Combination Formula: C(n,r) = n! / [r!(n-r)!]
When selecting r items from n total items where order doesn't matter:
C(n,r) = n! / [r! × (n-r)!]
Notice that C(n,r) = P(n,r) / r! because we divide by r! to eliminate duplicate orderings.
Important property: C(n,r) = C(n, n-r). For example, choosing 3 from 5 gives the same result as choosing 2 from 5 (both equal 10).
Problem 4: Team Selection Challenge
Question: From 10 employees, you need to select a 4-person project team. How many different teams are possible?
Solution:
- n = 10 (total employees)
- r = 4 (team size)
- C(10,4) = 10! / [4! × 6!] = 3,628,800 / [24 × 720] = 3,628,800 / 17,280 = 210 teams
Explanation: Unlike permutations, selecting {Alice, Bob, Carol, David} is the same as {David, Carol, Bob, Alice}.
Use our Combination Calculator for quick verification.
Problem 5: Lottery Probability
Question: What are the odds of winning a lottery where you pick 6 numbers from 49?
Solution:
- n = 49 (total numbers)
- r = 6 (numbers to pick)
- C(49,6) = 49! / [6! × 43!] = 13,983,816 combinations
Explanation: There are nearly 14 million different number combinations. Your odds of winning: 1 in 13,983,816 (0.0000072%).
This calculation demonstrates why lotteries are profitable—the house always has overwhelming odds.
Problem 6: Restaurant Menu Selection
Question: A restaurant offers 8 side dishes. If you can choose any 3 with your meal, how many different combinations exist?
Solution:
- n = 8 (total side dishes)
- r = 3 (dishes to select)
- C(8,3) = 8! / [3! × 5!] = 40,320 / [6 × 120] = 40,320 / 720 = 56 combinations
Explanation: Whether you pick {salad, fries, coleslaw} or {coleslaw, salad, fries}, it's the same meal combination.
Slug: permutation-combination-visual-comparison
Image Description:
- Main Focus: Side-by-side educational comparison diagram showing permutation vs combination concepts
- Key Elements:
- Left Panel (Permutation): Three podium levels labeled "1st", "2nd", "3rd" with different colored figures in specific positions, title "ORDER MATTERS" at top, P(n,r) formula below
- Right Panel (Combination): Same three colored figures arranged in a circle with no hierarchy, title "ORDER DOESN'T MATTER" at top, C(n,r) formula below
- Vertical dividing line in center with "VS" label
- Arrows showing how reordering changes permutation but not combination
- Clean infographic style with blue, red, yellow figures
- Setting: White background infographic, professional educational design
- Composition: Perfectly symmetrical split-screen layout, equal visual weight on both sides
- Technical Specs: High-contrast colors, vector-style clean graphics, educational illustration style
- Mood: Clear, instructive, making abstract mathematical concepts visually tangible
Section 3 — Advanced Applications: Complex Scenarios
Problem 7: Permutations with Repeated Elements
Question: How many distinct arrangements can you make with the letters in "MISSISSIPPI"?
Solution:
When elements repeat, use the formula: n! / (n₁! × n₂! × ... × nₖ!)
Where n₁, n₂, ... nₖ are the frequencies of repeated elements.
- Total letters: 11
- M: 1, I: 4, S: 4, P: 2
- Distinct arrangements = 11! / (1! × 4! × 4! × 2!) = 39,916,800 / (1 × 24 × 24 × 2) = 34,650 arrangements
Explanation: Without the division by repeated factorials, we'd overcount identical arrangements.
Problem 8: Circular Permutation Problem
Question: How many ways can 6 people sit around a circular table?
Solution:
For circular arrangements: (n-1)!
- Linear arrangements: 6! = 720
- Circular arrangements: (6-1)! = 5! = 120 ways
Explanation: In circular arrangements, rotations are considered identical. We fix one person's position and arrange the rest.
Bonus: If reflections are also considered identical (like with a necklace), divide by 2: 120 / 2 = 60.
Problem 9: Group Distribution Problem
Question: Divide 12 students into three groups of 4 each. How many ways can this be done?
Solution:
- First group: C(12,4)
- Second group: C(8,4)
- Third group: C(4,4)
- But groups are indistinguishable, so divide by 3!
Result = [C(12,4) × C(8,4) × C(4,4)] / 3! = [495 × 70 × 1] / 6 = 34,650 / 6 = 5,775 ways
Explanation: We divide by 3! because the groups themselves have no specific order or identity.
Explore more complex calculations with our Mathematical Tools Collection.
Problem 10: Restricted Permutation Challenge
Question: From 5 men and 4 women, how many ways can you form a committee of 3 men and 2 women?
Solution:
This requires both combinations:
- Select 3 men from 5: C(5,3) = 10
- Select 2 women from 4: C(4,2) = 6
- Total committees: 10 × 6 = 60 ways
Explanation: Use the multiplication principle: first select men, then women, and multiply the results.
Section 4 — Common Mistakes and Solutions
Problem 11: Misusing Permutation vs Combination
Common Error: Using permutation formula when order doesn't matter (or vice versa).
Example Problem: "Choose 3 books from 7 to pack for vacation."
❌ Wrong approach: P(7,3) = 210 (treating order as important)
✅ Correct approach: C(7,3) = 35 (order doesn't matter in packing)
Decision rule: Ask yourself: "If I swap two items, does it create a different outcome?" If no, use combinations.
Problem 12: Double-Counting Trap
Common Error: Counting the same arrangement multiple times in complex problems.
Example Problem: "Arrange 3 red balls and 2 blue balls in a row."
❌ Wrong approach: 5! = 120 (treats identical balls as distinct)
✅ Correct approach: 5! / (3! × 2!) = 120 / 12 = 10 arrangements (accounts for identical items)
Prevention tip: Always identify repeated elements and divide by their factorials.
For detailed explanations of factorial concepts, see our Factorial Calculation Logic & Applications Guide.
Slug: student-solving-permutation-combination-problems
Image Description:
- Main Focus: Young college student (Hispanic female, 20s, casual study clothes) concentrating at wooden desk solving math problems
- Key Elements:
- Open notebook with hand-drawn flowchart: "Does order matter? → YES: Use P(n,r) / NO: Use C(n,r)"
- Laptop screen showing factorial calculator with "C(10,4) = 210" result
- Multiple worked problems visible on paper with crossed-out mistakes and corrections
- Pencil in hand, actively writing
- Stack of math textbooks ("Combinatorics", "Discrete Math") on desk corner
- Coffee mug and highlighters scattered naturally
- Setting: Home study space or library, warm desk lamp illumination, bookshelf in soft-focus background
- Composition: Overhead 45-degree angle shot, showing notebook, laptop, and student's hands/upper body
- Technical Specs: Natural indoor lighting with warm desk lamp, sharp focus on notebook and screen, shallow depth of field
- Mood: Focused study session, problem-solving in action, educational determination
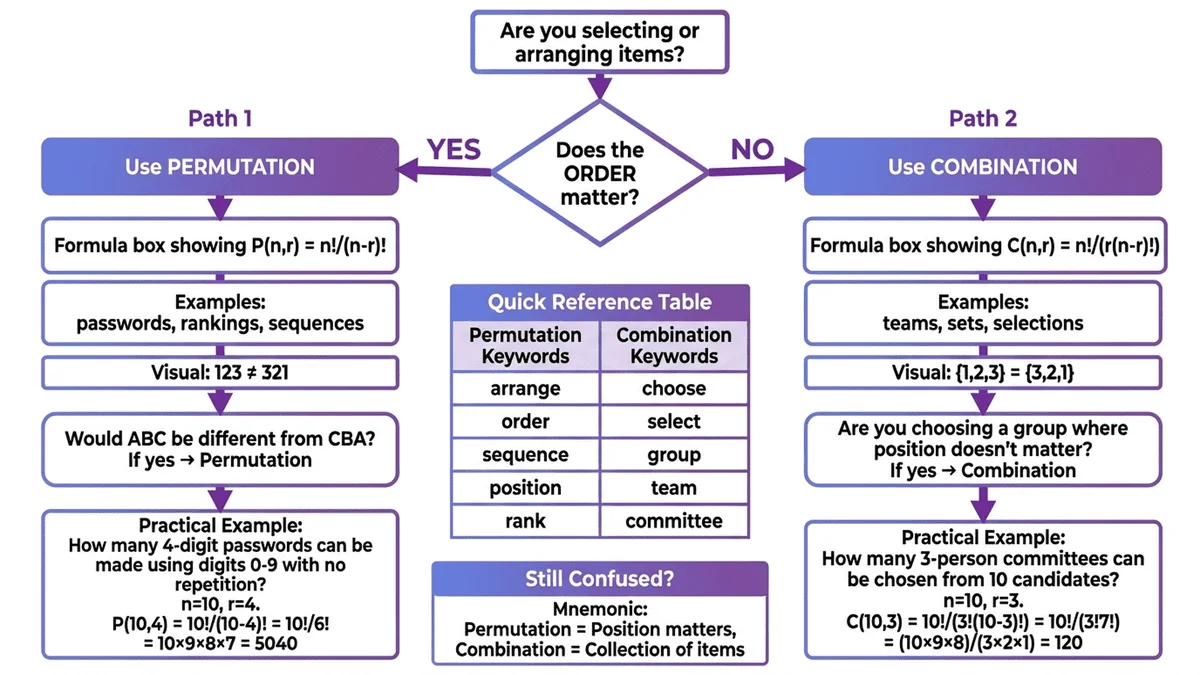
Quick Decision Checklist
Use this checklist to determine which formula to apply:
Use Permutations P(n,r) when:
- ✅ Assigning positions or ranks
- ✅ Creating sequences or passwords
- ✅ Order of selection matters
- ✅ ABC and BAC are different outcomes
Use Combinations C(n,r) when:
- ✅ Selecting team members
- ✅ Choosing items from a menu
- ✅ Order of selection doesn't matter
- ✅ ABC and BAC are the same outcome
Special formulas for:
- 🔁 Repeated elements: n! / (n₁! × n₂! × ...)
- ⭕ Circular arrangements: (n-1)!
- 👥 Group distributions: [C(n,r₁) × C(n-r₁,r₂) × ...] / k! (if groups are indistinguishable)
Still confused? Check our Factorial Calculation FAQ for answers to 15 common questions.
🚀 Master Permutation & Combination Calculations Instantly
Quick Fact: 90% of combinatorics students struggle with choosing the right formula—but with the right tools, you can solve complex problems in seconds instead of minutes.
How Tool Master Calculators Help You Excel
| Calculator | Perfect For | Time Saved |
|---|---|---|
| Factorial Calculator | Computing n! values up to 170! instantly | 5 minutes per calculation |
| Permutation Calculator | Solving P(n,r) problems with step-by-step explanations | 10 minutes per problem |
| Combination Calculator | Computing C(n,r) with detailed breakdowns | 10 minutes per problem |
✅ 100% Free: No registration, no hidden fees, unlimited calculations
✅ Privacy First: All calculations processed locally—your data never leaves your device
✅ Step-by-Step: Understand the logic behind every result with detailed explanations
✅ Mobile Optimized: Calculate on-the-go from any device
✅ Always Accurate: Verified algorithms eliminate human calculation errors
💡 Why Students & Professionals Choose Tool Master
- Students: Verify homework answers and prepare for exams with instant checking
- Teachers: Generate problem examples and demonstrate concepts in real-time
- Data Scientists: Calculate probability models and statistical distributions quickly
- Puzzle Enthusiasts: Solve combinatorial puzzles and brain teasers efficiently
Success Story: "I used to spend 20 minutes manually calculating lottery odds. Now it takes 10 seconds, and I can focus on understanding the concepts instead of arithmetic." — Sarah M., Statistics Student
👉 Try All Three Calculators Free Now!
Conclusion: Why Factorials Are the Heart of Combinatorics
Formula Quick Reference
Master these three essential formulas:
1. Permutation (order matters):
P(n,r) = n! / (n-r)!
2. Combination (order doesn't matter):
C(n,r) = n! / [r! × (n-r)!]
3. Permutation with repetition:
n! / (n₁! × n₂! × ... × nₖ!)
Remember: Combinations are always less than or equal to permutations for the same n and r, because C(n,r) = P(n,r) / r!.
Real-World Applications Summary
Throughout this guide, we solved 12 practical problems spanning:
Everyday scenarios: Wedding seating (120 arrangements), restaurant choices (56 combinations), team formation (210 teams)
Probability & statistics: Lottery odds (1 in 14 million), race outcomes (336 possibilities)
Complex arrangements: Circular seating (120 ways), group divisions (5,775 ways), repeated elements (34,650 distinct arrangements)
Security & cryptography: Password permutations (120 4-digit codes), access control systems
These applications demonstrate that factorial-based permutations and combinations aren't just abstract math—they're essential tools for analyzing real-world scenarios involving selection and arrangement.
Slug: formulas-written-paper-calculator-results
Image Description:
- Main Focus: Close-up of hands (mixed ethnicity, natural skin tone) writing mathematical formulas on lined notebook paper
- Key Elements:
- Paper clearly shows: "P(n,r) = n!/(n-r)!" and "C(n,r) = n!/[r!(n-r)!]" in neat handwriting
- Scientific calculator positioned to right showing "210" on LCD display
- Open textbook to left showing "Chapter 7: Combinatorics" page header and diagrams
- Black pen actively writing on paper
- Solved example: "C(10,4) = 10!/(4!×6!) = 210" with working shown
- Additional scratch work visible with factorial calculations
- Setting: Wooden study desk, natural window light from left side, soft shadows
- Composition: Overhead flat-lay shot, all elements arranged in triangular composition (paper center, calculator right, textbook left)
- Technical Specs: Sharp macro focus on handwriting and calculator display, warm natural lighting, slight paper texture visible
- Mood: Active learning, mathematical problem-solving, student study session
Further Learning Resources
Want to dive deeper? Explore these related factorial topics:
📖 Foundations: Build essential understanding with Factorial Calculation Logic & Applications: 7 Essential Use Cases from Math to Programming
📖 Quick Answers: Get instant clarification in Factorial Calculation FAQ: 15 Common Questions Answered
📖 History: Discover the fascinating evolution in History of Factorial: From Ancient Mathematics to Modern Computing
📖 Advanced Math: Extend factorials to continuous domains in Factorial & Gamma Function: Extending n! to Real Numbers
📖 Optimization: Master efficient computation in Factorial Calculation Optimization: 5 Methods to Compute Large Factorials Efficiently
📖 Programming: Implement factorials in 5 languages with Factorial in Programming: Implementation Guide for 5 Languages
🧮 Tools: Practice with our free Factorial Calculator, Permutation Calculator, Combination Calculator, and complete Mathematical Tools Collection
Pro tip: Bookmark our calculators and keep them handy for homework, exams, and professional projects. They're designed to save you time while helping you understand the underlying mathematics.
Whether you're a student mastering combinatorics, a teacher preparing lessons, or a professional solving real-world counting problems, factorial-based permutations and combinations give you the power to quantify possibilities and make informed decisions based on mathematical probability.
References
-
Rosen, K. H. (2019). Discrete Mathematics and Its Applications (8th ed.). McGraw-Hill Education. [Comprehensive textbook covering combinatorics, permutations, and combinations with extensive problem sets]
-
Graham, R. L., Knuth, D. E., & Patashnik, O. (1994). Concrete Mathematics: A Foundation for Computer Science (2nd ed.). Addison-Wesley. [Advanced treatment of factorial identities and combinatorial formulas]
-
Brualdi, R. A. (2010). Introductory Combinatorics (5th ed.). Pearson. [Focused resource on permutation and combination problems with applications]
-
National Institute of Standards and Technology (NIST). "Combinatorial Mathematics". NIST Digital Library of Mathematical Functions. https://dlmf.nist.gov/ [Authoritative reference for mathematical formulas and definitions]
-
Wolfram MathWorld. "Permutation" and "Combination". https://mathworld.wolfram.com/ [Comprehensive mathematical encyclopedia with worked examples]