階乘計算邏輯與應用指南
Factorial Calculation Logic & Applications: 7 Essential Use Cases from Math to Programming (2025)
Introduction: The Hidden Math Behind Everyday Decisions
Did you know your smartphone password has 3,628,800 possible combinations if it's 10 digits long?
That's 10 factorial (10!) at work.
In this guide, you'll master factorial calculation in 5 minutes—from basic math to real-world applications.
Factorials appear everywhere: password security, lottery odds, team arrangements, and computer algorithms. Understanding them gives you a powerful tool for solving counting problems quickly.
Whether you're a student tackling combinatorics homework, a developer optimizing algorithms, or just curious about the math behind everyday scenarios, this comprehensive guide covers everything you need.
What is Factorial? Understanding the Core Concept in 60 Seconds
Mathematical Definition and Notation
A factorial is the product of all positive integers from 1 up to a given number.
We write it with an exclamation mark: n!
The formula is simple:
n! = n × (n-1) × (n-2) × ... × 3 × 2 × 1
For example:
- 5! = 5 × 4 × 3 × 2 × 1 = 120
- 3! = 3 × 2 × 1 = 6
- 1! = 1
Special case: 0! = 1 (by mathematical convention, which we'll explain in the FAQ section)
This simple pattern powers complex calculations in probability, statistics, and computer science.
Visual Examples: From 3! to 10!
Let's see how factorials grow:
| n | n! | Calculation |
|---|---|---|
| 3 | 6 | 3 × 2 × 1 |
| 4 | 24 | 4 × 3 × 2 × 1 |
| 5 | 120 | 5 × 4 × 3 × 2 × 1 |
| 6 | 720 | 6 × 5 × 4 × 3 × 2 × 1 |
| 7 | 5,040 | 7 × 6 × 5 × 4 × 3 × 2 × 1 |
| 8 | 40,320 | 8! |
| 9 | 362,880 | 9! |
| 10 | 3,628,800 | 10! |
Notice how quickly the numbers explode.
This rapid growth is why factorials are perfect for counting arrangements and combinations.
Even a small increase (from 9 to 10) multiplies the result by 10, jumping from 362,880 to over 3.6 million.
3 Methods to Calculate Factorials
Method 1 - Manual Calculation Step-by-Step
Manual calculation works best for small numbers (up to 10).
Step-by-step example for 6!:
- Start with the number: 6
- Multiply by the next smaller number: 6 × 5 = 30
- Continue multiplying: 30 × 4 = 120
- Keep going: 120 × 3 = 360
- Almost done: 360 × 2 = 720
- Final step: 720 × 1 = 720
Result: 6! = 720
Limitation: Manual calculation becomes impractical for larger numbers. Calculating 20! by hand would take several minutes and is error-prone.
💡 Quick tip: Save time with our instant factorial calculator—get results in 0.1 seconds! Try calculating 20! now →
Method 2 - Using Online Factorial Calculator (Fastest Way)
For any factorial beyond 10, an online calculator is the most efficient choice.
Why use a calculator?
- ✓ Instant results for any number (even 100!)
- ✓ Zero calculation errors
- ✓ Step-by-step breakdown available
- ✓ Works for very large numbers that overflow standard calculators
How to use:
1. Visit the factorial calculator tool
2. Enter your number (e.g., 25)
3. Click "Calculate"
4. Get the result instantly: 25! = 15,511,210,043,330,985,984,000,000
The tool handles all the complexity, including very large numbers that would cause overflow errors in regular calculators.
Method 3 - Programming Implementation (JavaScript/Python)
For developers, implementing factorial in code is a common exercise.
JavaScript (Iterative):
function factorial(n) {
if (n === 0 || n === 1) return 1;
let result = 1;
for (let i = 2; i <= n; i++) {
result *= i;
}
return result;
}
console.log(factorial(5)); // Output: 120
Python (Recursive):
def factorial(n):
if n == 0 or n == 1:
return 1
return n * factorial(n - 1)
print(factorial(5)) # Output: 120
Key programming considerations:
- For n > 20, standard integers overflow—use BigInt (JavaScript) or Python's native large integers
- Recursive solutions are elegant but can cause stack overflow for very large n
- Memoization dramatically improves performance for repeated calculations
Want to see production-ready code? Check our factorial calculator technical documentation for optimized implementations with performance benchmarks →
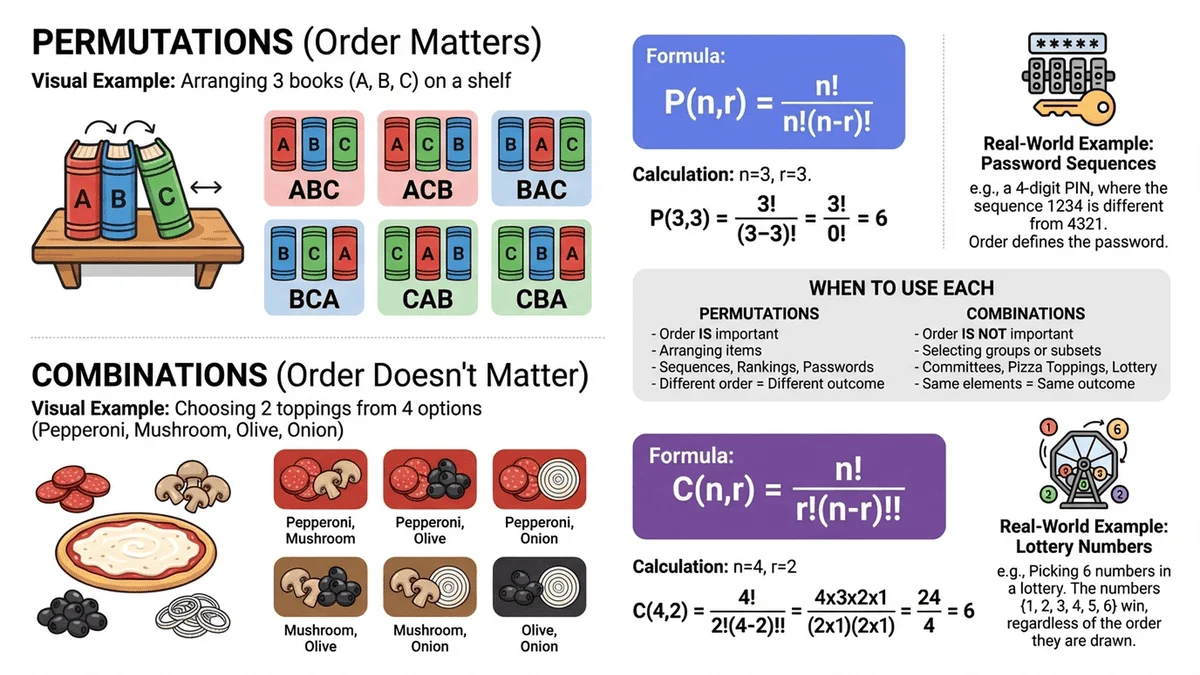
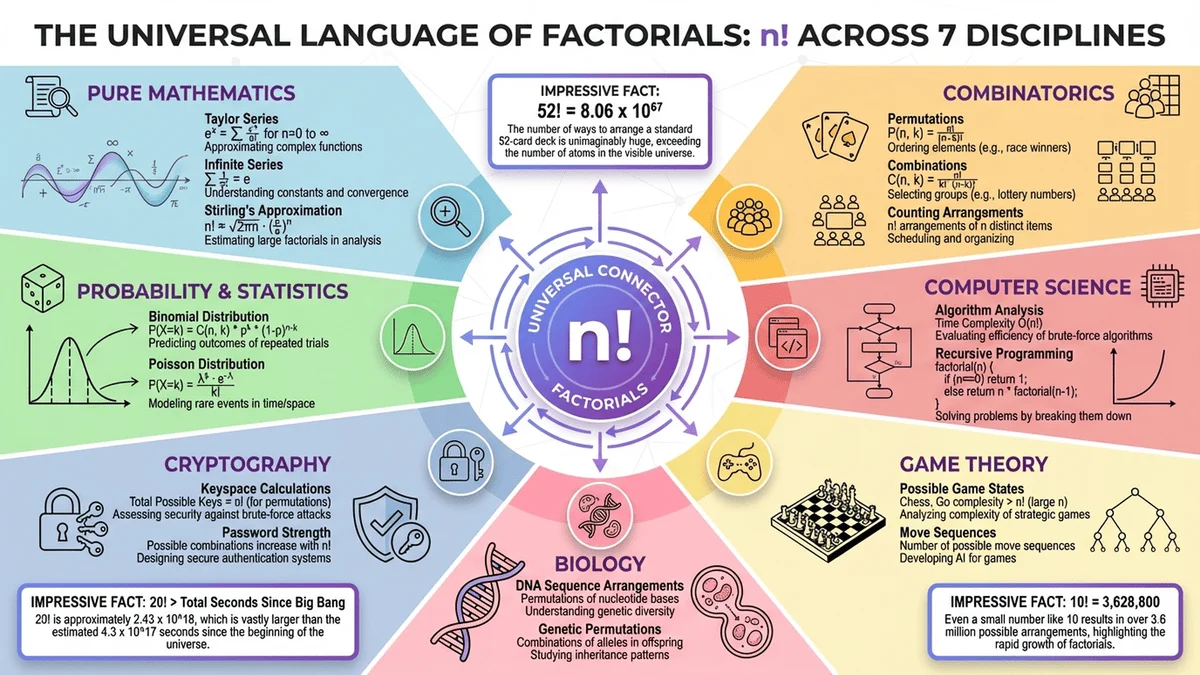
7 Real-World Factorial Applications You Use Daily
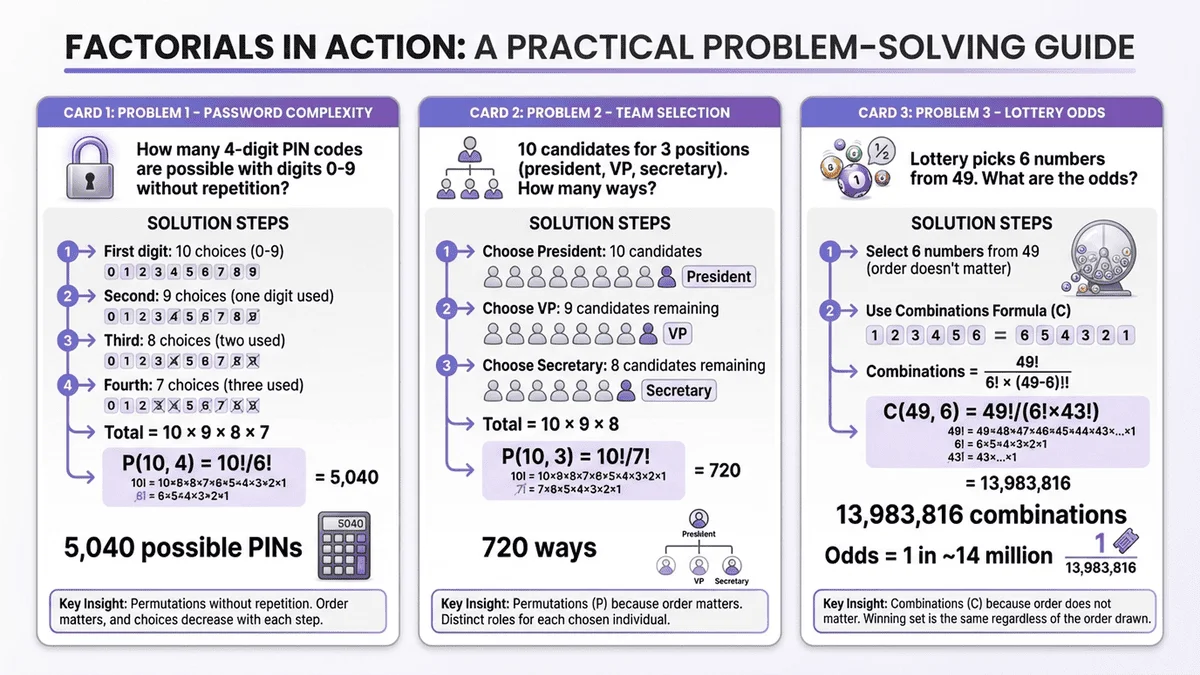
Application 1 - Password Security Combinations
How many possible arrangements exist for a 10-digit password?
Answer: 10! = 3,628,800 combinations
If you use all 10 digits (0-9) without repetition, a brute-force attack would need to try up to 3.6 million combinations.
Real-world impact:
- Longer passwords = exponentially more secure
- A 15-digit arrangement has 1.3 trillion (15!) combinations
- This is why security experts recommend longer, unique passwords
Use our password generator tool to create secure passwords with maximum combinations →
Application 2 - Lottery Probability Calculation
Ever wonder why lottery odds are so low?
Take a standard lottery: choose 6 numbers from 49.
The total combinations are calculated using factorials:
C(49,6) = 49! / (6! × 43!) = 13,983,816
That's nearly 14 million possible combinations for just one jackpot winner.
Key insight: Factorials explain why "beating the odds" in lotteries is mathematically improbable.
Application 3 - Team Arrangement Scenarios
A manager needs to arrange 5 team members in a presentation order.
How many possible arrangements?
5! = 120 different orders
Practical examples:
- Scheduling speakers for a 7-person panel: 7! = 5,040 arrangements
- Organizing a 4-person relay race: 4! = 24 possible lineups
- Seating 8 guests at a dinner table: 8! = 40,320 arrangements
Want to solve permutation problems instantly? Try our permutation and combination calculator →
Application 4 - Data Structure Algorithms
Factorials are fundamental in algorithm complexity analysis.
Examples:
- Traveling Salesman Problem: For n cities, there are (n-1)! / 2 possible routes
- Sorting algorithms: Worst-case scenarios for certain algorithms involve factorial time complexity
- Graph theory: Counting Hamiltonian paths requires factorial calculations
Understanding factorial growth helps developers choose efficient algorithms.
Application 5 - Statistical Analysis
Factorials appear in key statistical formulas:
- Permutations: P(n,r) = n! / (n-r)!
- Combinations: C(n,r) = n! / (r! × (n-r)!)
- Probability distributions: Binomial and multinomial distributions
- Chi-square tests: Degrees of freedom calculations
These formulas power everything from clinical trials to A/B testing in marketing.
Application 6 - Game Theory
Board games, card games, and strategy games rely heavily on factorial math.
Card shuffling: A standard 52-card deck can be arranged in 52! ways.
That's approximately 8 × 10^67 combinations—more than atoms in the Milky Way!
Chess: The number of possible chess games is astronomical, partly due to factorial calculations of move sequences.
Application 7 - Cryptography Systems
Modern encryption uses factorial-based permutations for key generation.
RSA encryption and other cryptographic algorithms depend on:
- Large number factorizations
- Permutation-based key spaces
- Factorial growth ensuring massive key combinations
The security of your online banking and private messages relies on these mathematical principles.
🎯 Recommended Tool Combination
When working with factorials and counting problems, these tools can dramatically boost your efficiency:
| Tool | Purpose | Key Feature |
|---|---|---|
| Factorial Calculator | Calculate n! instantly | Handles up to 170! |
| Permutation & Combination Calculator | Arrangement problems | P(n,r) and C(n,r) formulas |
| Prime Checker | Number theory | Prime factorization support |
💡 Pro Tip: All tools are completely free and process data locally in your browser for privacy.
Advanced Topics: Large Factorial Optimization & Stirling Approximation
Why 100! Requires Special Handling
Standard calculators fail at 70! because the numbers become astronomically large.
100! = 9.33 × 10^157
That's a 158-digit number!
Challenges:
- Integer overflow in most programming languages
- Memory limitations
- Precision loss in floating-point arithmetic
Solutions:
- Use arbitrary-precision libraries (BigInt in JavaScript, native in Python)
- Apply logarithms: log(n!) = log(1) + log(2) + ... + log(n)
- Implement Stirling's approximation for estimates
Stirling Approximation Formula Explained
For very large factorials, we don't always need exact values—estimates work fine.
Stirling's Formula:
n! ≈ √(2πn) × (n/e)^n
Where:
- π ≈ 3.14159
- e ≈ 2.71828
Accuracy:
- For n = 10: Error < 1%
- For n = 100: Error < 0.01%
- As n grows, the approximation becomes nearly exact
Use cases:
- Statistical calculations requiring only magnitude
- Algorithm complexity analysis (Big O notation)
- Physics and chemistry computations
Programming Optimization Techniques
When calculating factorials in production code, optimization matters.
7 key techniques:
- Memoization: Cache previously calculated values
- Tail recursion: Avoid stack overflow
- Iterative approach: More memory-efficient than recursion
- Logarithmic factorial: Use log(n!) for very large n
- Stirling's approximation: When exact values aren't needed
- BigInt/arbitrary precision: Handle factorials beyond standard integer limits
- Parallel computing: Distribute multiplication across processors
Learn all 5 optimization methods in depth with code examples and performance benchmarks: Factorial Calculation Optimization: 5 Methods to Compute Large Factorials Efficiently →
Common Mistakes and How to Avoid Them
Mistake 1 - Confusing Factorial with Exponentiation
Wrong: 5! = 5^5 = 3,125
Correct: 5! = 5 × 4 × 3 × 2 × 1 = 120
Factorials multiply descending integers, not the same number repeatedly.
Memory trick: The exclamation mark (!) means "multiply ALL the way down to 1."
Mistake 2 - Overflow Errors in Large Calculations
The problem: Calculating 100! in Excel or basic calculators often returns "#NUM!" or "Infinity."
Why it happens: Most systems can't store numbers larger than 10^308.
Solution:
- Use specialized tools like our factorial calculator
- In programming, use BigInt (JavaScript) or Python's native integers
- Apply Stirling's approximation if estimates suffice
Real example: Our calculator handles up to 170! accurately—try it yourself →
Mistake 3 - Negative Number Factorial Myths
Question: What is (-5)! ?
Answer: Factorials are undefined for negative integers.
The factorial function only works for non-negative integers (0, 1, 2, 3...).
However: The Gamma function extends factorials to real and complex numbers, allowing calculations like (0.5)!
Curious about extending factorials beyond integers? Discover how the Gamma function enables calculating (0.5)! and more: Factorial & Gamma Function: Extending n! to Real Numbers (Complete 2025 Guide) →
Try It Now: Free Online Factorial Calculator
Features: Instant Results, Step-by-Step Breakdown, Batch Processing
Our factorial calculator offers everything you need for quick, accurate calculations.
🚀 Key Features:
✓ Calculate up to 170! instantly - handles massive numbers without overflow
✓ Step-by-step breakdown - see the complete multiplication process
✓ Batch processing - calculate multiple factorials at once
✓ Export results - save as CSV or copy to clipboard
✓ 100% local processing - your data never leaves your browser
✓ Mobile-friendly - works perfectly on phones and tablets
✓ No registration required - start using immediately
How it works:
- Enter any number from 0 to 170
- Click "Calculate"
- Get instant results with full precision
- View step-by-step breakdown (optional)
- Export or share results
Perfect for:
- Students: homework and exam preparation
- Developers: algorithm testing and debugging
- Researchers: statistical calculations
- Teachers: creating example problems
- Anyone: solving everyday counting problems
→ Launch Factorial Calculator Now
Further Reading: Deep Dive into Mathematical Foundations
📚 Related Articles to Expand Your Knowledge
Ready to master factorial calculations and related mathematical concepts? Explore these comprehensive guides:
Core Factorial Resources:
- Factorial Calculation FAQ: 15 Common Questions Answered (0! to 170! Explained) - Get instant answers to the top 15 factorial questions including "Why is 0! = 1?" and calculation methods
- History of Factorial: From Ancient Mathematics to Modern Computing - Trace the 2,500-year journey from ancient Indian combinatorics to Christian Kramp's exclamation mark notation
Advanced Applications:
- Factorial in Permutations & Combinations: 12 Real-World Problems Solved - Master counting problems from wedding seating arrangements to lottery odds with step-by-step solutions
- Factorial Calculation Optimization: 5 Methods to Compute Large Factorials Efficiently - Learn memoization, logarithmic calculation, Stirling's approximation, big integers, and parallel computing
Mathematical Extensions:
- Factorial & Gamma Function: Extending n! to Real Numbers (Complete 2025 Guide) - Discover how to calculate 0.5! ≈ 0.886 and extend factorials to continuous domains
- Factorial in Programming: Implementation Guide for 5 Languages (Python, JavaScript, Java, C++, Go) - Production-ready factorial implementations with error handling and optimization
🔢 Explore More Math Tools
Factorial calculator is just the beginning. Discover 5 more powerful math tools:
Related calculators:
- Prime Checker - Test primality and find prime factors
- GCD & LCM Calculator - Greatest common divisor and least common multiple
- Permutation & Combination Calculator - P(n,r) and C(n,r) formulas
- Base Converter - Binary, octal, decimal, hexadecimal conversion
- Random Number Generator - Cryptographically secure randomness
Conclusion: Your Factorial Mastery Checklist
What You've Learned
In this comprehensive guide, you've mastered:
✅ Factorial fundamentals - Mathematical definition and notation (n!)
✅ 3 calculation methods - Manual, calculator, and programming approaches
✅ 7 real-world applications - From passwords to cryptography
✅ Advanced techniques - Stirling's approximation and optimization
✅ Common pitfalls - How to avoid factorial mistakes
✅ Practical tools - Free calculator for instant results
Next Steps
To continue your learning journey:
- Bookmark the factorial calculator for quick access to instant calculations
- Explore permutation problems to apply factorials in real scenarios
- Read the FAQ guide to solidify your understanding of edge cases
- Dive into programming implementations if you're a developer
💡 Final Reminder
Tool Master provides 33 professional tools across 8 categories.
All tools are:
- ✓ 100% free - no hidden fees or premium tiers
- ✓ Privacy-focused - local processing, no data sent to servers
- ✓ No registration - start using immediately
- ✓ Mobile-friendly - works on all devices
If this guide helped you, bookmark Tool Master and share it with friends who need reliable online tools!
References
- Wolfram MathWorld, "Factorial" - Comprehensive mathematical reference
- NIST Digital Library of Mathematical Functions - Factorial and Gamma function definitions
- Khan Academy, "Permutations and Combinations" course - Educational foundation
- MDN Web Docs, "BigInt" - JavaScript large integer handling
- OEIS Foundation, "Factorial numbers" - Integer sequence database
- Wikipedia, "Factorial" - Historical context and applications
- Stack Overflow, "Calculating large factorials" - Programming discussions
- Journal of Statistical Software, "Special Functions in R" - Gamma function implementations
- Concrete Mathematics (Graham, Knuth, Patashnik) - Chapter on factorials
- The Art of Computer Programming, Vol. 1 (Donald Knuth) - Algorithm analysis