🌍 數字系統歷史:從羅馬到阿拉伯
從古羅馬的累加系統到印度-阿拉伯的位值制革命, 探索人類數字記數法的演進歷程與文明智慧的結晶。

1. 數字系統演進史 📜
人類數字記數法的里程碑
數字系統的發展反映了人類文明的進步。從簡單的計數刻痕到複雜的位值制, 每一次革新都極大地推動了數學、科學與商業的發展。
🏺 巴比倫六十進位制
古巴比倫人發明了六十進位制(Sexagesimal), 使用楔形文字符號表示 1-59。這一系統至今仍影響我們的時間計量(60 秒 = 1 分鐘)。
- 基數:60
- 符號:楔形文字(⚑ = 1,⚏ = 10)
- 優勢:60 有多個因數(1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30)
- 局限:缺少「零」的概念(用空位表示)
🏛️ 羅馬數字系統
古羅馬發展出累加減法制,使用 7 個基本符號(I, V, X, L, C, D, M)。 這一系統在歐洲統治千年,直到阿拉伯數字引入。
- 基數:10(但非位值制)
- 符號:7 個拉丁字母
- 優勢:易於雕刻、書寫簡單
- 局限:無零、無法表示大數、運算複雜
🔢 中文數字系統
中國發展出十進位制與位值制雛形, 使用算籌(counting rods)進行計算,是世界上最早的位值制系統之一。
- 基數:10
- 符號:一、二、三、四、五、六、七、八、九、十、百、千、萬
- 優勢:口語表達清晰、數字概念明確
- 特色:使用「空位」表示零(算籌系統)
🌟 印度-阿拉伯數字革命
印度數學家發明了真正的零和位值制, 阿拉伯人將其傳播到歐洲,徹底改變了數學運算的方式。
- 基數:10(十進位制)
- 符號:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- 革命性創新:零作為獨立數字與佔位符
- 優勢:運算高效、可表示任意大小的數
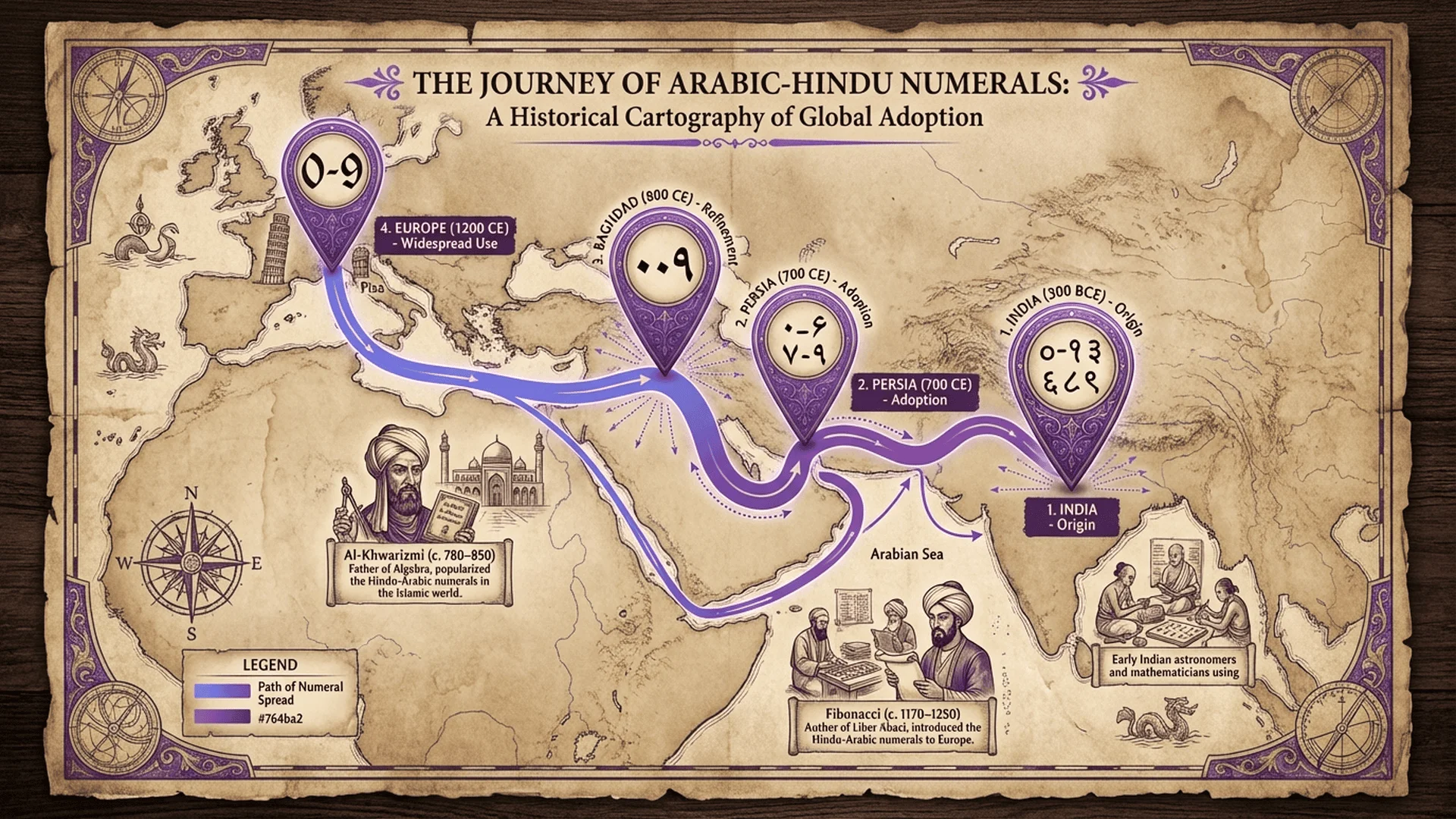
🇪🇺 阿拉伯數字傳入歐洲
數學家斐波那契(Fibonacci)在《算盤書》(Liber Abaci, 1202) 中介紹印度-阿拉伯數字系統,逐漸取代羅馬數字成為主流。
2. 羅馬數字系統:規則與局限性 🏛️
羅馬數字的核心規則
羅馬數字使用累加減法制,通過符號的組合與位置關係表達數值:
🔹 基本規則
- 累加規則:較大符號在前,較小符號在後 → 相加(如 VI = 5 + 1 = 6)
- 減法規則:較小符號在前,較大符號在後 → 相減(如 IV = 5 - 1 = 4)
- 重複規則:相同符號最多連續 3 次(如 III = 3,IIII 錯誤)
- 減法限制:只能用於特定組合(IV, IX, XL, XC, CD, CM)
範例對比:
| 數字 | 羅馬數字 | 分解 |
|---|---|---|
| 1994 | MCMXCIV |
M(1000) + CM(900) + XC(90) + IV(4) |
| 2024 | MMXXIV |
MM(2000) + XX(20) + IV(4) |
| 444 | CDXLIV |
CD(400) + XL(40) + IV(4) |
羅馬數字的致命缺陷
❌ 缺陷 1:無法表示零
羅馬數字沒有「零」的概念,無法表示「無」或「空位」。 這導致位值制無法實現,進而限制了大數運算。
❌ 缺陷 2:運算極度複雜
嘗試用羅馬數字進行乘法:
XVIII × XIV = ?
(18 × 14 = 252 = CCLII)
幾乎不可能直接計算!
❌ 缺陷 3:表示範圍有限
標準羅馬數字只能表示 1-3999。
超過 3999 需要使用特殊符號(如上劃線表示 ×1000),
但這並非標準化系統。
❌ 缺陷 4:無法表示分數與小數
古羅馬使用獨立的分數系統(如 uncia = 1/12), 但無法表示任意精度的小數,限制了科學計算的發展。

3. 阿拉伯數字系統:位值制與零的發明 🌟
位值制的革命性創新
印度-阿拉伯數字系統的核心是位值制(Positional Notation), 數字的值不僅取決於符號本身,還取決於其位置。
位值制範例:
數字 5,237 的位值分解:
- 5 在千位 → 5 × 10³ = 5,000
- 2 在百位 → 2 × 10² = 200
- 3 在十位 → 3 × 10¹ = 30
- 7 在個位 → 7 × 10⁰ = 7
- 總和:5,000 + 200 + 30 + 7 = 5,237
零的雙重角色
「零」(0)是人類數學史上最偉大的發明之一,具有兩個關鍵角色:
🔹 角色 1:佔位符(Placeholder)
零用於表示「空位」,區分不同位值的數字。
例如:
105 = 1 個百、0 個十、5 個個位
150 = 1 個百、5 個十、0 個個位
沒有零,這兩個數字無法區分!
🔹 角色 2:獨立數字(Number)
零本身是一個數字,表示「無」或「空集合」。
這使得數學運算更加完整:
5 - 5 = 0(減法的封閉性)
0 × 任意數 = 0(乘法單位元)
💡 零的發明時間線
- 公元 3 世紀:印度數學家首次使用點(·)表示空位
- 公元 5 世紀:印度數學家阿耶波多(Aryabhata)將零視為獨立數字
- 公元 7 世紀:婆羅摩笈多(Brahmagupta)定義零的運算規則
- 公元 9 世紀:阿拉伯數學家花拉子米(Al-Khwarizmi)將零引入代數
- 公元 13 世紀:斐波那契將零帶入歐洲
位值制的運算優勢
位值制使得四則運算變得簡單高效:
🆚 加法對比
| 系統 | 範例 | 難度 |
|---|---|---|
| 羅馬數字 | MCMXCIV + XXVI = ?(1994 + 26 = 2020) |
❌ 極度困難 |
| 阿拉伯數字 | 1994 + 26 = 2020(直式運算) |
✅ 簡單 |
🆚 乘法對比
| 系統 | 範例 | 難度 |
|---|---|---|
| 羅馬數字 | XVIII × XIV = ?(18 × 14 = 252) |
❌ 幾乎不可能 |
| 阿拉伯數字 | 18 × 14 = 252(直式運算) |
✅ 簡單 |
4. 其他數字系統 🌐
瑪雅數字:二十進位制
瑪雅文明發展出獨立的二十進位制(Vigesimal), 並且獨立發明了零(使用貝殼符號 🐚 表示)。
瑪雅數字特點:
- 基數:20(人類手指 + 腳趾總數)
- 符號:點(·= 1)、橫線(— = 5)、貝殼(🐚 = 0)
- 位值:垂直排列,從下往上依次為 1, 20, 400, 8000...
- 範例:
🐚 → 0 × 400 = 0 — → 5 × 20 = 100 ·· → 2 × 1 = 2 總計:102
中文數字:混合位值制
中文數字系統使用十進位制,並結合權位系統(十、百、千、萬)。
中文數字特點:
- 基數:10
- 符號:一、二、三、四、五、六、七、八、九 + 十、百、千、萬
- 表示法:數字 + 權位(如「三千五百」= 3500)
- 優勢:口語表達清晰,數字概念明確
- 2024 = 二千零二十四
- 305 = 三百零五(「零」表示空位)
- 10,000 = 一萬(使用萬進制)
巴比倫數字:六十進位制
古巴比倫的六十進位制至今仍影響我們的時間與角度計量。
巴比倫數字特點:
- 基數:60
- 符號:楔形文字(⚑ = 1,⚏ = 10)
- 優勢:60 有眾多因數(1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30),便於分數計算
- 遺產:
- 時間:60 秒 = 1 分鐘,60 分鐘 = 1 小時
- 角度:360° = 6 × 60°(圓周分為 360 度)
5. 數字系統對比分析 📊
| 系統 | 基數 | 位值制 | 有零 | 運算效率 | 現代應用 |
|---|---|---|---|---|---|
| 羅馬數字 | 10 | ❌ | ❌ | ⭐ 極低 | 儀式性、裝飾性 |
| 阿拉伯數字 | 10 | ✅ | ✅ | ⭐⭐⭐⭐⭐ 極高 | 全球標準 |
| 瑪雅數字 | 20 | ✅ | ✅ | ⭐⭐⭐⭐ 高 | 歷史研究 |
| 中文數字 | 10 | ✅(混合) | ✅ | ⭐⭐⭐ 中等 | 中文書寫、財務 |
| 巴比倫數字 | 60 | ✅ | ❌(空位) | ⭐⭐ 低 | 時間、角度計量 |
為什麼阿拉伯數字成為全球標準?
✅ 優勢 1:運算高效
位值制配合零的使用,使得加減乘除運算變得簡單高效,極大降低了學習與計算成本。
✅ 優勢 2:表示範圍無限
理論上可以表示任意大小的數字,只需增加位數。相比羅馬數字的 1-3999 限制,靈活性大幅提升。
✅ 優勢 3:科學計算友好
可表示小數、分數、負數、科學記號,是現代科學與工程的基礎。
✅ 優勢 4:易於標準化
僅需 10 個符號(0-9),易於印刷、教學與全球推廣。
6. 現代應用場景 🎯
不同數字系統的當代用途
🏛️ 羅馬數字
- 建築年份標記(如 ©MMXXIV)
- 書籍章節編號(前言使用 i, ii, iii)
- 電影片尾字幕年份
- 鐘錶錶盤數字(傳統美學)
- 王室名稱(如 Elizabeth II)
🌍 阿拉伯數字
- 科學計算與工程設計
- 金融交易與會計記錄
- 電腦程式設計(二進制基礎)
- 日常計數與商業活動
- 全球統一的數學語言
🇨🇳 中文數字
- 財務支票大寫(壹、貳、叁,防偽)
- 傳統文化場合(春聯、詩詞)
- 法律文件正式寫法
- 農曆日期表示
🕐 巴比倫六十進位制
- 時間計量(60 秒、60 分鐘)
- 角度測量(360° = 6×60°)
- 地理坐標(經緯度)
- 天文學(時角、赤緯)
數字系統的未來
儘管阿拉伯數字已成為全球標準,但在特定領域,其他數字系統仍保有其文化與實用價值。 未來,隨著量子計算與人工智慧的發展,我們可能會看到新的數字表示法出現, 以適應更高維度的計算需求。
💡 有趣的事實
- 💻 電腦使用二進制:所有數字最終以 0 和 1 儲存
- 🧬 DNA 編碼:使用四進制(A, T, C, G)
- 🎶 音樂記譜:使用十二平均律(12 進制)
- 🌈 顏色表示:十六進制(Hex,如 #FF5733)
🚀 立即試用羅馬數字轉換器
體驗羅馬數字與阿拉伯數字的雙向轉換,深入了解兩種數字系統的差異。
立即使用工具