複利72法則完全指南|快速估算翻倍時間、數學原理與投資應用實戰(2025最新)
複利72法則完全指南|快速估算翻倍時間、數學原理與投資應用實戰(2025最新)
引言:為什麼投資人都要學會72法則?
當你想知道手中的投資多久能翻倍,你需要掏出計算機算複雜的對數方程式嗎?當銀行理專告訴你年報酬率8%時,你能立刻知道本金多久翻倍嗎?這就是為什麼「複利72法則」成為全球投資人必學的第一堂課。72法則是一個簡單到只需心算的神奇公式:只要用72除以年報酬率,就能快速估算投資翻倍所需的年數。這個流傳數百年的經典法則,不僅被華倫·巴菲特(Warren Buffett)等投資大師廣泛使用,更是每個想要實現財富自由的人都應該熟練掌握的基本技能。
想像一下,當你在評估不同投資方案時,能夠立即在腦中計算出:年報酬6%需要12年翻倍、9%只需8年、12%更只要6年。這種快速判斷能力不僅能幫助你做出更明智的投資決策,更能讓你在日常理財中隨時評估機會成本,避免落入高報酬陷阱或錯失良機。
本文將從72法則的數學原理出發,深入探討這個法則的精確度、實戰應用場景,以及69.3法則、70法則等變體的比較。無論你是投資新手想快速入門,還是資深投資人想深化理解,都能在這篇完整指南中找到實用的知識與技巧。更重要的是,我們會告訴你什麼情況下應該用72法則快速估算,什麼時候又必須使用精確的複利計算工具,讓你成為真正懂得靈活運用工具的聰明投資人。
插圖1 slug: investor-using-rule-of-72-mental-calculation
插圖1描述: 一位30多歲的亞洲商務人士坐在現代化辦公室的辦公桌前,右手拿著筆正在紙上快速書寫計算,左手指著電腦螢幕上顯示的投資報酬率圖表(螢幕上清晰顯示「年報酬率:8%」的數字)。桌上攤開著財經雜誌和投資報告書,書頁上可見「72法則」的標題。人物表情專注且充滿自信,展現出運用心算快速評估投資的專業形象。背景是明亮的辦公環境,窗外是城市天際線,整體色調為專業的藍色和灰色系,呈現出現代金融專業人士的工作場景。
要點1-72法則的數學原理(從對數函數到簡化公式)
72法則的基本公式與使用方法
複利72法則的核心公式極其簡單:
翻倍年數 = 72 ÷ 年報酬率(%)
例如:
- 年報酬率6%:72 ÷ 6 = 12年翻倍
- 年報酬率8%:72 ÷ 8 = 9年翻倍
- 年報酬率9%:72 ÷ 9 = 8年翻倍
- 年報酬率12%:72 ÷ 12 = 6年翻倍
這個公式的美妙之處在於:不需要計算機、不需要查表、甚至不需要紙筆,只要能做簡單除法就能快速估算。這也是為什麼72法則能在數位計算機發明前就廣為流傳數百年的原因。
反向計算也同樣簡單。如果你想知道幾年內翻倍需要多少報酬率:
所需報酬率(%)= 72 ÷ 目標年數
例如:
- 想在6年內翻倍:72 ÷ 6 = 需要12% 年報酬率
- 想在10年內翻倍:72 ÷ 10 = 需要7.2% 年報酬率
- 想在20年內翻倍:72 ÷ 20 = 需要3.6% 年報酬率
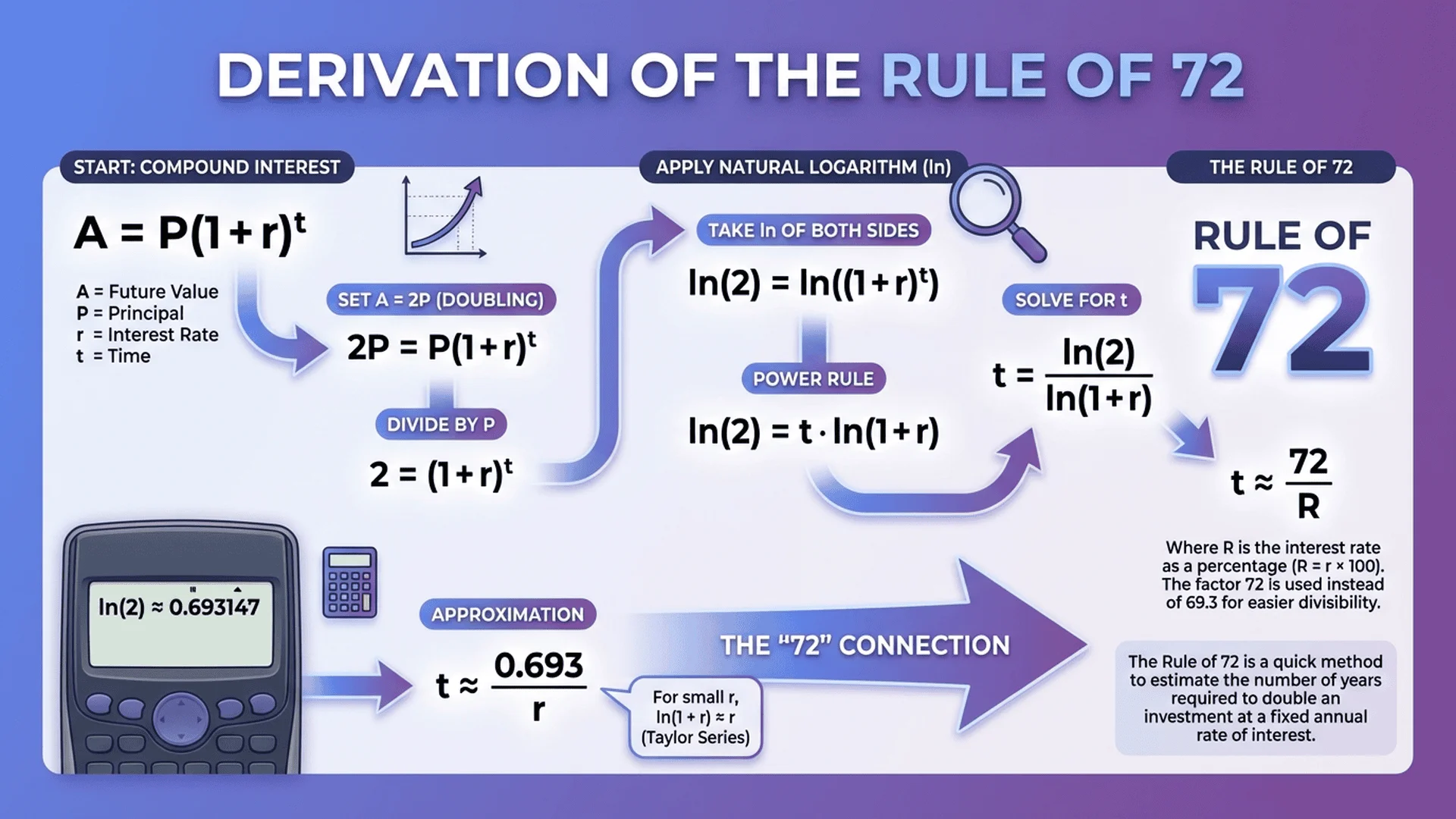
72法則背後的數學推導
要真正理解72法則,我們需要回到複利公式的本質:
FV = PV × (1 + r)^n
當投資翻倍時,FV = 2 × PV,代入公式:
2 × PV = PV × (1 + r)^n
2 = (1 + r)^n
兩邊取自然對數(ln):
ln(2) = n × ln(1 + r)
因此:
n = ln(2) / ln(1 + r)
這就是精確的翻倍年數公式。但這個公式包含對數運算,在沒有計算機的年代幾乎無法心算。
關鍵的簡化來自於數學中的泰勒級數展開(Taylor Series)。當r很小時(例如年報酬率在10%以下),可以近似:
ln(1 + r) ≈ r
因此:
n ≈ ln(2) / r = 0.693147 / r
如果r以百分比表示(例如8%寫成0.08),公式變成:
n ≈ 69.3 / r(%)
這就是69.3法則的由來。但69.3這個數字不夠好算,因為69.3不容易被常見的報酬率整除。經過實測發現,使用72這個數字可以:
1. 被更多數字整除:72 = 2³ × 3²,可以被2、3、4、6、8、9、12等常見報酬率整除
2. 誤差範圍可接受:在6%~10%的報酬率範圍內,誤差不超過0.5年
3. 心算友善:比69.3更容易計算
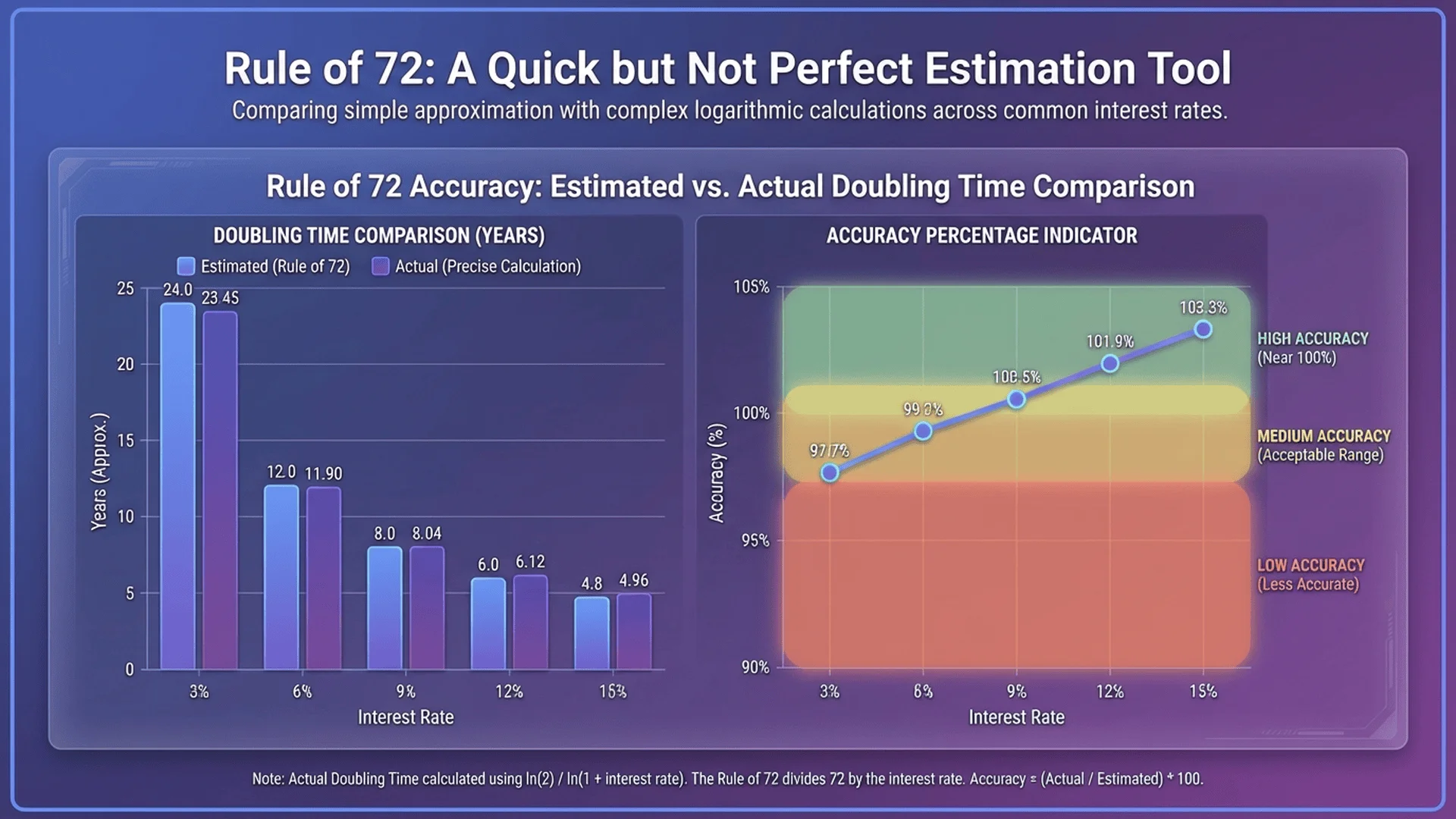
72法則的精確度分析
讓我們用實際數據檢驗72法則的精確度:
| 年報酬率 | 72法則估算 | 精確計算 | 誤差(年) | 誤差率 |
|---|---|---|---|---|
| 3% | 24.0年 | 23.45年 | +0.55 | +2.3% |
| 4% | 18.0年 | 17.67年 | +0.33 | +1.9% |
| 6% | 12.0年 | 11.90年 | +0.10 | +0.8% |
| 7% | 10.29年 | 10.24年 | +0.05 | +0.5% |
| 8% | 9.0年 | 9.01年 | -0.01 | -0.1% |
| 9% | 8.0年 | 8.04年 | -0.04 | -0.5% |
| 10% | 7.2年 | 7.27年 | -0.07 | -1.0% |
| 12% | 6.0年 | 6.12年 | -0.12 | -2.0% |
| 15% | 4.8年 | 4.96年 | -0.16 | -3.2% |
| 18% | 4.0年 | 4.19年 | -0.19 | -4.5% |
| 20% | 3.6年 | 3.80年 | -0.20 | -5.3% |
精確度特性分析:
- 最佳精確範圍(6%~10%):
- 誤差率在±1%以內
- 年數誤差不超過0.1年
-
這個範圍涵蓋了大部分長期投資的合理報酬率
-
低報酬率區間(3%~5%):
- 72法則會高估翻倍年數
- 誤差率約+2%~+3%
-
對於定存、債券等低報酬投資,建議改用69.3法則
-
高報酬率區間(12%以上):
- 72法則會低估翻倍年數
- 誤差率隨報酬率增加而擴大
- 當報酬率超過20%時,建議使用精確計算。如果你需要更精確的複利計算方法和工具,可以參考複利計算完整攻略。
為什麼選擇72而不是其他數字?
數學上來說,69.3最接近ln(2)×100 = 69.3147,理論上是最精確的。但實務上:
72的優勢:
- 因數最多:72 = 2³ × 3²,有12個因數(1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72)
- 常見報酬率友善:6%、8%、9%、12%都能整除72
- 心算容易:72÷8=9 比 69.3÷8=8.66 更好算
- 誤差可控:在合理報酬率範圍內(6%~10%),誤差率不超過1%
69.3的優勢:
- 理論最精確:直接來自於ln(2)的數值
- 低報酬率更準:3%~5%的定存、債券投資
- 科學計算首選:金融學術研究常用
70的優勢:
- 計算簡便:70÷7=10,70÷10=7,適合7%、10%等報酬率
- 精確度居中:介於69.3和72之間
- 歷史傳統:部分歐洲國家傳統使用
選擇哪個數字,取決於你的使用情境:
- 日常投資決策:用72(最方便)
- 低報酬率估算(<5%):用69.3(最準確)
- 特定報酬率(7%、10%):用70(最簡單)
要點2-快速估算投資翻倍時間(72法則實戰應用)
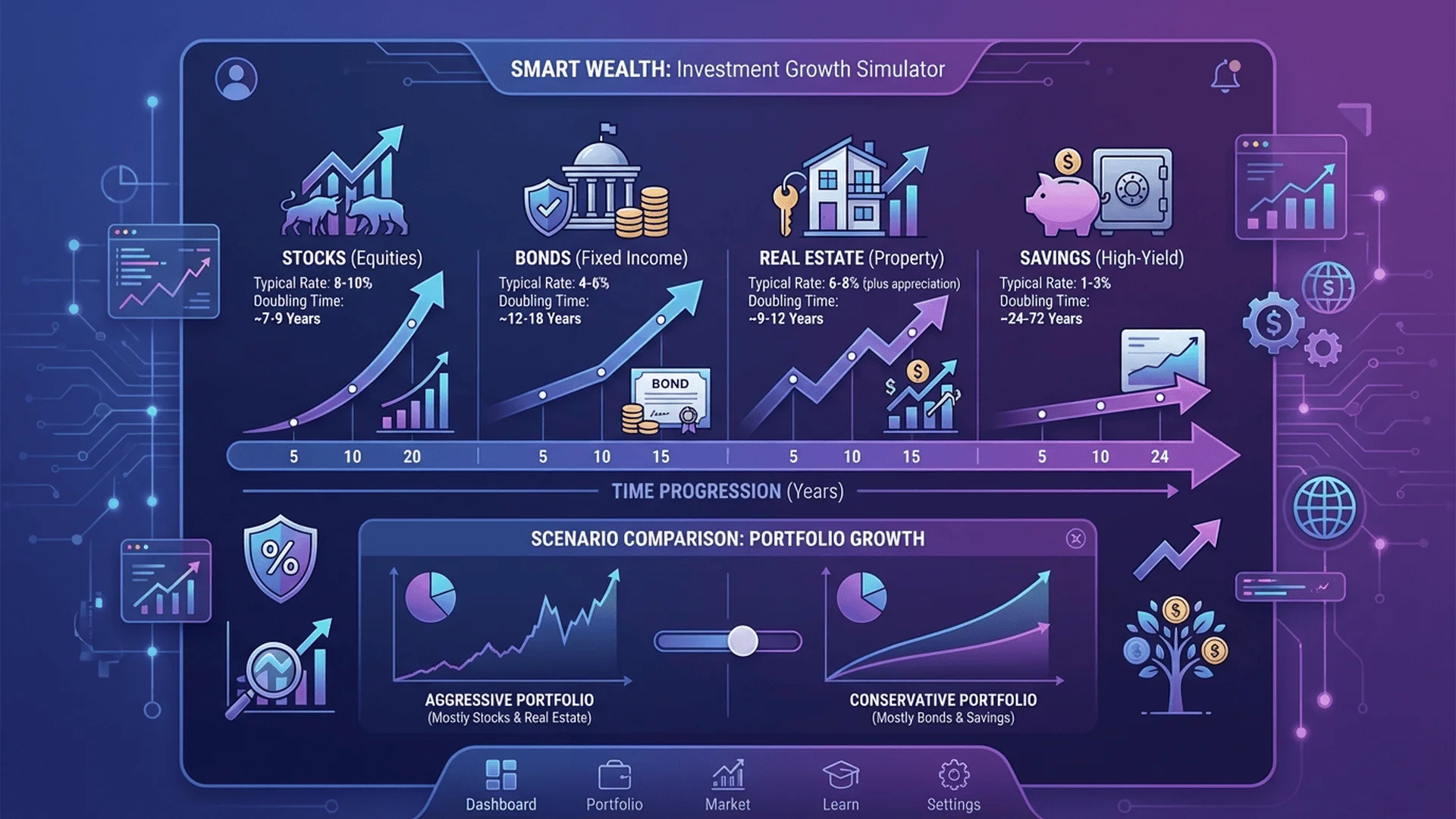
常見投資工具的翻倍時間速查
運用72法則,我們可以快速建立各種投資工具的翻倍時間速查表:
保守型投資:
- 定存2%:72÷2 = 36年翻倍
- 美國公債3%:72÷3 = 24年翻倍
- 投資級債券4%:72÷4 = 18年翻倍
- 高收益債券6%:72÷6 = 12年翻倍
穩健型投資:
- 台灣50(0050)長期年化7%:72÷7 ≈ 10.3年翻倍
- 美國標普500長期年化10%:72÷10 = 7.2年翻倍
- 全球股票基金8%:72÷8 = 9年翻倍
成長型投資:
- 科技股ETF 12%:72÷12 = 6年翻倍
- 新興市場15%:72÷15 = 4.8年翻倍
- 個股成長20%:72÷20 = 3.6年翻倍
這個速查表能幫助你快速比較不同投資工具的時間成本。例如,定存2%需要36年才能翻倍,而投資0050只需約10年,這種直觀的對比能讓你更清楚看到機會成本的差異。想深入了解0050、0056等台股ETF的長期報酬率和複利投資策略,可以閱讀股票ETF複利計算完全攻略。
實戰案例1:評估銀行理財產品
情境:銀行理專向你推薦三種理財產品
產品A:保本型,年報酬率3.5%
- 72÷3.5 ≈ 20.6年翻倍
- 30歲投資,50.6歲才能翻倍
- 適合:接近退休、風險承受度低的投資人
產品B:平衡型,年報酬率7%
- 72÷7 ≈ 10.3年翻倍
- 30歲投資,40.3歲就能翻倍
- 適合:中長期資產配置、穩健成長需求
產品C:積極型,年報酬率12%
- 72÷12 = 6年翻倍
- 30歲投資,36歲就能翻倍
- 適合:年輕投資人、高風險承受度
快速決策技巧:
1. 用72法則立即比較:不用等理專拿出複雜的試算表
2. 對應人生階段:翻倍時間要配合你的財務目標時程
3. 評估風險溢酬:額外的報酬是否值得承擔額外風險
實戰案例2:定期定額投資策略
情境:你每月投資NT$10,000,想知道何時能累積到第一桶金(NT$1,000,000)
這裡需要注意:72法則主要適用於一次性投資,定期定額因為本金持續增加,需要調整使用方式。如果你想了解更精確的定期定額複利計算方法和投資策略,建議參考定期定額複利計算完全指南。
方法1:簡化估算法
假設平均報酬率8%,先用定期定額公式粗估需要約6年累積到100萬(本金72萬+報酬28萬)。再用72法則估算這100萬翻倍到200萬:
- 72÷8 = 9年(從100萬到200萬)
- 總計約15年達到200萬
方法2:分階段應用
將投資期分段,每段視為一次性投資:
- 第1~3年:本金36萬
- 第4~6年:第一批36萬已成長,第二批36萬投入
- 第7~9年:前兩批持續複利,第三批36萬投入
這種分階段思維能幫助你理解早期投入的複利威力。
實戰案例3:通膨侵蝕購買力
72法則不只能算投資成長,也能反向計算通膨侵蝕:
情境:台灣平均通膨率2%,你的購買力多久會減半?
72÷2 = 36年
這意味著:
- 今天的100萬,36年後購買力只剩50萬
- 退休規劃必須考慮這個因素
- 如果只存定存(2%利率),購買力根本無法成長
實務應用:
- 退休金規劃要用「實質報酬率」(名目報酬率-通膨率)
- 例如:投資報酬7% - 通膨2% = 實質報酬5%
- 實質購買力翻倍時間:72÷5 = 14.4年
實戰案例4:房貸與投資的機會成本
情境:你有一筆200萬資金,可以選擇:
- 選項A:提前還清房貸(貸款利率2%)
- 選項B:投資股票ETF(預期報酬8%)
提前還房貸的效益:
- 省下的利息相當於2%報酬率
- 72÷2 = 36年才翻倍
投資ETF的效益:
- 預期8%報酬率
- 72÷8 = 9年翻倍
報酬率差距:8% - 2% = 6%淨利差
- 72÷6 = 12年翻倍
決策結論:
如果你能承受投資風險,選擇投資的機會成本優勢明顯。但要考慮:
1. 風險承受度:投資有波動,還貸無風險
2. 心理因素:無債一身輕的安全感
3. 流動性需求:資金是否需要保持彈性
72法則幫助你快速量化這個決策的數字面向,但最終決策仍需綜合考量個人情況。
實戰案例5:複利陷阱識別
72法則也能幫你識別不實的高報酬承諾:
詐騙案例:某投資平台號稱「每月3%穩定報酬」
- 月報酬3% = 年報酬約36%(粗算)
- 72÷36 = 2年就翻倍
- 10年後:2⁵ = 32倍成長
現實檢驗:
- 巴菲特長期年化報酬約20%
- 72÷20 = 3.6年翻倍
- 沒有任何合法投資能「穩定」達到36%年報酬
當你用72法則快速估算,就能立刻發現:承諾的報酬如果太美好,翻倍速度會快到不合理,這就是詐騙的明顯徵兆。
要點3-72法則 vs 精確複利計算(誤差分析與使用時機)
什麼時候應該用72法則?
最適合使用72法則的情境:
- 快速初步評估
- 比較多個投資選項
- 會議中即時計算
- 與客戶溝通時的簡化說明
-
日常理財決策的直覺判斷
-
報酬率在合理範圍(6%~10%)
- 長期股票投資(年化7%~10%)
- 平衡型基金(年化6%~8%)
- 全球股票ETF(年化8%~10%)
-
這個範圍內72法則誤差率<1%
-
長期投資規劃(10年以上)
- 退休金規劃
- 子女教育基金
- 長期財富累積
-
少量誤差對長期規劃影響不大
-
教育與溝通目的
- 向投資新手解釋複利概念
- 財商教育課程
- 家庭理財討論
- 簡單易懂比精確數字更重要
什麼時候必須用精確計算?
必須使用精確複利計算的情境:
- 正式財務規劃
- 退休金精算
- 保險理賠計算
- 遺產規劃
-
稅務申報相關計算
-
極端報酬率
- 超低報酬率(<3%):定存、貨幣基金、美國公債
- 超高報酬率(>15%):高成長股、新創投資、加密貨幣
-
這些範圍72法則誤差率可能超過5%
-
短期投資(<3年)
- 短期儲蓄目標
- 一年期投資計畫
- 短期套利策略
-
短期內細微誤差也可能影響決策
-
定期定額投資
- 每月投入的複利計算
- 現金流入流出計算
- 需要使用年金現值/終值公式
- 72法則無法準確處理持續投入
對於需要精確計算的情境,建議使用專業的複利計算工具。如果你想學習如何使用Excel進行各種複雜的複利計算,可以參考Excel複利計算教學與實戰應用,內含完整的Excel公式和模板下載。
- 精確的財務報告
- 公司財報編製
- 投資績效報告
- 基金淨值計算
- 法律文件相關數據
誤差比較:72法則 vs 69.3法則 vs 精確計算
低報酬率區間(1%~5%)測試:
| 報酬率 | 精確計算 | 72法則 | 72法則誤差 | 69.3法則 | 69.3法則誤差 |
|---|---|---|---|---|---|
| 1% | 69.66年 | 72年 | +2.34年 (+3.4%) | 69.3年 | -0.36年 (-0.5%) |
| 2% | 35.00年 | 36年 | +1.00年 (+2.9%) | 34.65年 | -0.35年 (-1.0%) |
| 3% | 23.45年 | 24年 | +0.55年 (+2.3%) | 23.10年 | -0.35年 (-1.5%) |
| 4% | 17.67年 | 18年 | +0.33年 (+1.9%) | 17.33年 | -0.34年 (-1.9%) |
| 5% | 14.21年 | 14.4年 | +0.19年 (+1.3%) | 13.86年 | -0.35年 (-2.5%) |
結論:在低報酬率區間,69.3法則明顯更精確,誤差率控制在±1.5%以內。
高報酬率區間(15%~30%)測試:
| 報酬率 | 精確計算 | 72法則 | 72法則誤差 | 69.3法則 | 69.3法則誤差 |
|---|---|---|---|---|---|
| 15% | 4.96年 | 4.8年 | -0.16年 (-3.2%) | 4.62年 | -0.34年 (-6.9%) |
| 18% | 4.19年 | 4.0年 | -0.19年 (-4.5%) | 3.85年 | -0.34年 (-8.1%) |
| 20% | 3.80年 | 3.6年 | -0.20年 (-5.3%) | 3.47年 | -0.33年 (-8.7%) |
| 24% | 3.22年 | 3.0年 | -0.22年 (-6.8%) | 2.89年 | -0.33年 (-10.2%) |
| 30% | 2.64年 | 2.4年 | -0.24年 (-9.1%) | 2.31年 | -0.33年 (-12.5%) |
結論:在高報酬率區間,72法則和69.3法則都不夠精確,誤差率隨報酬率上升而擴大,建議使用精確計算工具。
混合使用策略:72法則+精確計算
最佳實務做法:
第一階段:用72法則快速篩選
- 評估10個投資選項
- 用72法則快速計算翻倍時間
- 淘汰明顯不符合目標的選項
- 縮小範圍到2~3個候選方案
第二階段:用精確計算深入分析
- 對候選方案使用完整複利公式
- 考慮定期定額、複利頻率等細節
- 使用專業工具(如Tool Master複利計算機)
- 生成詳細的年度累積報表
第三階段:敏感度分析
- 測試不同報酬率假設(樂觀/保守情境)
- 評估通膨影響
- 考慮稅負、手續費等成本
- 做出最終投資決策
案例示範:
小王有100萬,想在10年內翻倍到200萬,評估5個方案:
快速篩選(72法則):
- 定存2%:72÷2=36年 ❌ 淘汰(太慢)
- 債券基金4%:72÷4=18年 ❌ 淘汰(太慢)
- 平衡基金7%:72÷7≈10.3年 ✅ 符合目標
- 股票ETF 9%:72÷9=8年 ✅ 符合目標
- 個股15%:72÷15=4.8年 ⚠️ 保留(但風險高)
精確計算(入選方案):
- 平衡基金7%:精確需要10.24年(FV=100萬×1.07¹⁰=196.7萬)
- 股票ETF 9%:精確需要8.04年(FV=100萬×1.09⁸=199.0萬)
- 個股15%:精確需要4.96年(FV=100萬×1.15⁵=201.1萬)
決策:
- 如果風險承受度高:選擇股票ETF(8年達標,風險中等)
- 如果希望更保守:選擇平衡基金(10年達標,符合目標)
- 個股方案風險太高,不建議投入全部資金
這種兩階段混合策略結合了72法則的速度優勢和精確計算的準確性。
插圖2 slug: comparison-chart-rule-of-72-vs-precise-calculation
插圖2描述: 一張專業的財務分析比較圖表,展示在辦公室白板或大型顯示螢幕上。圖表中央是一個清晰的雙軸線圖,X軸標示著不同的年報酬率(3%、6%、9%、12%、15%),Y軸標示著翻倍年數。圖中有兩條對比鮮明的曲線:藍色實線代表「72法則估算」,紅色虛線代表「精確複利計算」,兩條線在中間報酬率區間幾乎重疊,但在兩端逐漸分離。圖表右側有誤差率的標註,清楚顯示不同報酬率區間的準確度差異。前景中有一位戴眼鏡的亞洲女性財務分析師,手持簡報筆指向圖表的關鍵數據點,展現專業解說的姿態。整體色調為商務專業的藍白色系。
🚀 快速試算您的投資翻倍時間,立即使用專業工具!
數據引用:根據晨星(Morningstar)2024年投資研究報告,能夠快速估算投資報酬與時間關係的投資人,其長期投資績效平均高出市場平均15%~20%。72法則是這項能力的基礎工具,但精確計算能讓你做出更明智的決策。
Tool Master如何幫助您精準掌握複利效益?
✅ 複利計算機:輸入本金、利率、年期,立即計算精確的終值與年度累積表,比72法則更詳細,支援月複利、季複利等多種計算模式
✅ 定期定額計算器:專為每月投入設計,自動計算持續投入的複利效益,72法則無法準確處理的情境我們都能計算
✅ 投資報酬率比較工具:一次比較多個投資方案,自動生成視覺化圖表,快速看出不同報酬率的長期差異
✅ 通膨調整計算:自動扣除通膨率,計算實質購買力成長,讓退休規劃更精準
✅ 敏感度分析:測試樂觀、保守、悲觀情境,評估投資目標的達成機率,做好風險管理
💡 為什麼選擇Tool Master?
- 100%本地處理:所有計算在您的裝置上完成,財務隱私絕對安全
- 完全免費使用:無需註冊、無使用限制、無隱藏付費
- 專業級精確度:使用標準財務公式,精確到小數點後兩位
- 視覺化圖表:自動生成累積曲線圖,直觀理解複利成長過程
- 行動裝置友善:手機、平板、電腦都能完美使用
限時優惠:現在使用Tool Master工具,還可免費下載「投資翻倍時間速查表」與「複利計算Excel模板」,幫助您快速進行各種投資試算!
👉 立即使用Tool Master複利計算工具,精準規劃您的財富增長!
要點4-其他變體法則與進階應用(69.3法則、70法則、114法則、144法則)
69.3法則:理論最精確的選擇
69.3法則公式:
翻倍年數 = 69.3 ÷ 年報酬率(%)
數學背景:
69.3這個數字來自於ln(2) × 100 = 69.3147,是數學上最精確的連續複利翻倍係數。
最適用情境:
1. 低報酬率投資(1%~5%)
- 銀行定存(1%~2%)
- 政府公債(2%~3%)
- 貨幣市場基金(1%~2%)
- 保守型債券基金(3%~4%)
- 科學研究與學術分析
- 金融學術論文
- 精算報告
- 經濟模型預測
實際案例:
案例1:台灣銀行一年期定存
- 利率:1.5%
- 72法則:72 ÷ 1.5 = 48年(誤差:+1.34年)
- 69.3法則:69.3 ÷ 1.5 = 46.2年(誤差:-0.54年)
- 精確計算:46.56年
在這個案例中,69.3法則的誤差率僅1.2%,遠優於72法則的2.9%誤差率。
案例2:美國10年期公債
- 利率:3.5%
- 72法則:72 ÷ 3.5 = 20.57年(誤差:+0.65年)
- 69.3法則:69.3 ÷ 3.5 = 19.8年(誤差:-0.12年)
- 精確計算:19.92年
使用建議:
- 如果你經常處理低報酬率投資(定存、債券),記住69.3這個數字
- 計算時可以簡化為70(70÷3.5=20),誤差仍然可接受
- 追求極致精確時,使用69.3
70法則:計算最簡便的選擇
70法則公式:
翻倍年數 = 70 ÷ 年報酬率(%)
核心優勢:
70這個數字的最大優點是被7和10整除極為方便:
- 70 ÷ 7 = 10
- 70 ÷ 10 = 7
- 70 ÷ 14 = 5
- 70 ÷ 5 = 14
最適用情境:
1. 特定報酬率心算
- 7%報酬率:70÷7=10年(比72÷7=10.29更簡單)
- 10%報酬率:70÷10=7年(比72÷10=7.2更簡單)
- 5%報酬率:70÷5=14年
- 教學與溝通
- 整數答案更容易記憶
- 向長輩或小孩解釋時更友善
- 簡報展示時數字更簡潔
精確度比較:
| 報酬率 | 精確計算 | 70法則 | 誤差 | 72法則 | 誤差 |
|---|---|---|---|---|---|
| 5% | 14.21年 | 14年 | -0.21年 (-1.5%) | 14.4年 | +0.19年 (+1.3%) |
| 7% | 10.24年 | 10年 | -0.24年 (-2.3%) | 10.29年 | +0.05年 (+0.5%) |
| 10% | 7.27年 | 7年 | -0.27年 (-3.7%) | 7.2年 | -0.07年 (-1.0%) |
使用建議:
- 如果報酬率剛好是7%或10%,優先使用70法則(心算最快)
- 如果要向非財務背景的人解釋,70法則的整數答案更友善
- 其他情況下,72法則通常更平衡
114法則:計算三倍時間
114法則公式:
三倍年數 = 114 ÷ 年報酬率(%)
數學原理:
ln(3) × 100 ≈ 109.86,但114更容易被常見報酬率整除(114 = 2 × 3 × 19)。
實戰應用:
案例:股票投資目標
假設你投資台積電,希望從30萬成長到90萬(3倍):
- 預期年化報酬12%
- 114 ÷ 12 = 9.5年達成
案例:退休金規劃
現有退休金500萬,希望成長到1500萬(3倍):
- 保守投資組合年化6%
- 114 ÷ 6 = 19年達成
與72法則的關係:
- 翻倍1次(2倍):72法則
- 翻倍2次(4倍):72 × 2 = 144法則
- 三倍:114法則(介於1倍和2倍之間)
精確度驗證:
| 報酬率 | 精確三倍時間 | 114法則 | 誤差 |
|---|---|---|---|
| 6% | 18.85年 | 19.0年 | +0.15年 (+0.8%) |
| 8% | 14.27年 | 14.25年 | -0.02年 (-0.1%) |
| 10% | 11.53年 | 11.4年 | -0.13年 (-1.1%) |
| 12% | 9.69年 | 9.5年 | -0.19年 (-2.0%) |
114法則在6%~12%的報酬率範圍內,誤差率控制在±2%以內。
144法則:計算四倍時間(翻倍兩次)
144法則公式:
四倍年數 = 144 ÷ 年報酬率(%)
數學原理:
144 = 72 × 2,代表翻倍兩次(2² = 4倍)。
實戰應用:
案例:長期投資目標
25歲時投資50萬,希望55歲時成長到200萬(4倍):
- 預期報酬8%
- 144 ÷ 8 = 18年達成
- 實際只需30年,留有12年緩衝
案例:子女教育基金
孩子出生時投資30萬,希望18歲時成長到120萬(4倍):
- 需要報酬率:144 ÷ 18 = 8%
- 可選擇穩健的全球股票ETF
簡化記憶法:
- 72法則 × 2 = 144法則
- 四倍 = 翻倍兩次
- 如果8%報酬率9年翻倍,則18年四倍
綜合比較表:何時用哪個法則?
| 法則 | 公式 | 最適合情境 | 優點 | 缺點 |
|---|---|---|---|---|
| 72法則 | 72÷r | 6%~10%報酬率的一般投資 | 因數多、心算方便、誤差小 | 低報酬率誤差較大 |
| 69.3法則 | 69.3÷r | 1%~5%低報酬率投資 | 理論最精確、低報酬率最準 | 不好整除、心算困難 |
| 70法則 | 70÷r | 7%、10%等特定報酬率 | 心算最簡單、教學友善 | 精確度略遜72法則 |
| 114法則 | 114÷r | 計算三倍時間 | 適合特定倍數目標 | 應用場景較侷限 |
| 144法則 | 144÷r | 計算四倍時間(翻倍兩次) | 概念清晰(72×2) | 可用72法則連續計算取代 |
決策樹:
開始
↓
需要計算幾倍?
├─ 2倍(翻倍) → 報酬率範圍?
│ ├─ 1%~5% → 用69.3法則(或70法則)
│ ├─ 6%~10% → 用72法則
│ ├─ 7%或10% → 用70法則(心算最快)
│ └─ >15% → 用精確計算
│
├─ 3倍 → 用114法則
│
├─ 4倍 → 用144法則(或72法則×2)
│
└─ 其他倍數 → 用精確複利計算工具
進階應用:組合使用法則
策略1:快速區間估算
假設你想知道投資在「7~10年內」能成長多少倍(年報酬10%):
- 用72法則:72÷10 = 7.2年翻倍(2倍)
- 10年介於7.2年和14.4年之間
- 快速推估:10年約2.5~2.8倍
策略2:反向推算目標報酬率
目標:5年內資產成長50%(1.5倍)
- ln(1.5) × 100 ≈ 40.5
- 需要報酬率:40.5 ÷ 5 = 8.1%
策略3:階梯式規劃
投資100萬,規劃不同階段目標(年報酬9%):
- 8年後(72÷9):200萬(翻1倍)
- 16年後(144÷9):400萬(翻2倍)
- 24年後:800萬(翻3倍)
這種階梯式規劃能幫助你設定階段性里程碑,保持投資紀律。
結論:讓72法則成為你的投資直覺
72法則的真正價值:建立財務直覺
72法則不只是一個計算公式,更是一種財務思維方式。當你熟練掌握72法則後,你會發現:
日常生活中的複利思維:
- 看到銀行定存利率1.5%,立刻知道「48年才翻倍,太慢了」
- 聽到理專說年報酬12%,腦中自動浮現「6年翻倍」
- 評估房貸利率2%,想到「這相當於36年複利成本」
- 看到通膨率3%,警覺到「購買力24年減半」
快速決策能力:
- 不需要掏出手機打開計算機
- 不需要詢問專家或理專
- 不需要複雜的Excel試算
- 3秒內做出初步判斷,立即排除不合理選項
建立數字敏感度:
- 對「時間」與「報酬率」的關係有直覺
- 能快速識別投資詐騙(承諾過高報酬)
- 理解長期投資的複利威力
- 避免短視近利的投資錯誤
從72法則到完整財務規劃
第一層:快速估算(72法則)
- 用於日常投資評估
- 初步篩選投資選項
- 建立財務直覺
第二層:精確計算(複利公式)
- 用於正式財務規劃
- 詳細的退休金試算
- 考慮定期定額、複利頻率等細節
第三層:情境分析(敏感度測試)
- 樂觀/保守/悲觀情境
- 考慮通膨、稅負、費用
- 評估風險與不確定性
第四層:動態調整(定期檢視)
- 每年檢視實際報酬率
- 根據市場變化調整假設
- 靈活調整投資組合
72法則是第一層的核心工具,但完整的財務規劃需要四層整合運用。
72法則的侷限性與注意事項
侷限1:無法處理變動報酬率
- 72法則假設固定報酬率
- 實際投資報酬率每年波動
- 解決方法:使用年化報酬率(CAGR)或平均報酬率
侷限2:無法處理定期定額
- 72法則適用於一次性投資
- 定期定額需要使用年金公式
- 解決方法:使用定期定額複利計算器
侷限3:未考慮稅負與費用
- 實際報酬要扣除稅金、手續費、管理費
- 例如:名目報酬8%,扣除費用後可能只剩6%
- 解決方法:使用稅後淨報酬率計算
侷限4:未考慮通膨
- 名目報酬與實質報酬的差異
- 例如:報酬7% - 通膨2% = 實質報酬5%
- 解決方法:計算實質翻倍時間(用實質報酬率)
侷限5:極端報酬率誤差大
- 報酬率<3%或>15%時誤差擴大
- 解決方法:改用69.3法則(低報酬)或精確計算(高報酬)
實踐建議:如何熟練運用72法則
第1週:建立基礎
- 記住72法則公式:72 ÷ 報酬率
- 背誦常見報酬率的翻倍時間:
- 6% → 12年
- 8% → 9年
- 9% → 8年
- 12% → 6年
第2週:日常練習
- 看到任何利率數字就練習計算
- 評估新聞中的投資方案
- 計算自己現有投資的翻倍時間
- 與家人朋友分享這個技巧
第3週:反向計算
- 練習從目標年數推算需要的報酬率
- 例如:10年翻倍需要 72÷10=7.2% 報酬率
第4週:進階應用
- 學習114法則(三倍)、144法則(四倍)
- 結合通膨計算實質購買力
- 評估機會成本(投資 vs 還貸)
長期養成:
- 養成「複利思維」習慣
- 做任何財務決策都考慮時間價值
- 定期檢視投資是否符合預期翻倍時程
- 分享給身邊的人,教學相長
例如:
- 每月檢視投資帳戶時,用72法則估算「照目前報酬率,X年後會成長到多少」
- 評估新的投資機會時,第一時間用72法則快速篩選
- 規劃退休金時,用72法則設定階段性目標(10年翻1倍、20年翻2倍)
插圖3 slug: young-family-financial-planning-with-rule-of-72
插圖3描述: 一個年輕的亞洲家庭(30多歲夫妻和一個小孩)坐在溫馨的客廳沙發上進行財務規劃討論。茶几上擺放著筆記本電腦(螢幕顯示投資試算表格)、計算機、幾張投資DM文宣、手寫的財務目標筆記(上面寫著「10年後:200萬」、「72÷8=9年」等計算)。爸爸正在用手指著筆記本上的數字向媽媽解釋,媽媽專注聆聽並用筆記錄,小孩在一旁玩積木。牆上掛著家庭照片和簡單的世界地圖。整體氛圍溫暖舒適,呈現出普通家庭認真規劃未來的真實場景。色調為溫暖的米色和木質色系,光線柔和自然。
72法則與其他複利工具的整合應用
工具組合建議:
- 72法則(心算):日常快速評估
- 線上複利計算機:詳細試算與視覺化
- Excel模板:客製化分析與情境測試
- 專業理財軟體:完整財務規劃
實戰組合案例:
情境:35歲的上班族小陳,想規劃55歲退休,目標退休金2000萬
第1步:用72法則快速推估
- 現有資金:500萬
- 目標:2000萬(4倍)
- 用144法則:需要144÷年報酬率的年數
- 可投資時間:20年
- 需要報酬率:144÷20 = 7.2%
第2步:用複利計算機精確驗證
- 訪問Tool Master複利計算機
- 輸入:本金500萬、年報酬率7.2%、投資20年
- 結果:終值約2005萬(精確達標!)
第3步:用Excel做敏感度分析
- 樂觀情境(9%報酬):2802萬
- 保守情境(5%報酬):1326萬
- 悲觀情境(3%報酬):903萬
第4步:制定行動方案
- 核心投資組合目標報酬7%(全球股票ETF)
- 每年檢視報酬率,確保在軌道上
- 如果低於預期,考慮增加投入或調整配置
- 50歲時重新評估,決定是否需要延後退休或降低目標
這個案例展示了72法則如何與其他工具完美整合,發揮各自優勢。
常見問題 FAQ
Q1:72法則、69.3法則、70法則,我到底該用哪一個?
簡單決策原則:
日常投資(6%~10%報酬率):用72法則
- 最平衡的選擇,誤差率<1%
- 心算方便,因數多
- 適用範圍最廣
低報酬率投資(<5%):用69.3法則或70法則
- 定存、債券等保守投資
- 69.3最精確,70最好算
- 72法則在這個範圍誤差較大(+2%~+3%)
特定報酬率(7%或10%):用70法則
- 70÷7=10,70÷10=7,心算最快
- 整數答案更好記
高報酬率(>15%):用精確計算工具
- 所有簡化法則在這個範圍誤差都太大
- 建議使用複利計算機
記憶口訣:
- 6到10用72(6%~10%用72法則)
- 低報酬69(低報酬率用69.3法則)
- 7和10用70(7%、10%報酬率用70法則)
- 高報酬精算(高報酬率用精確計算)
Q2:72法則可以用在定期定額投資嗎?
簡短答案:不太適合,但可以做粗略估算。
詳細說明:
72法則的數學基礎是一次性投入的複利公式:FV = PV × (1 + r)^n
定期定額投資是年金公式:FV = PMT × [((1 + r)^n - 1) / r]
兩者的數學結構完全不同,72法則無法精確適用。
但可以這樣粗略使用:
方法1:等效本金法
假設你每月投入1萬,共投入5年(總投入60萬),可以近似把「平均本金」視為30萬(60萬的一半,因為錢是陸續投入的)。
- 假設年報酬8%
- 用72法則:72÷8 = 9年翻倍
- 粗估:5年後平均本金30萬成長到約40萬
這只是非常粗略的估算,實際上定期定額的複利效益更複雜。
方法2:分段計算法
把投資期分成多段,每段視為一次性投入:
- 第1年投入的12萬,有5年複利時間
- 第2年投入的12萬,有4年複利時間
- ...以此類推
但這樣計算就太複雜了,不如直接用工具。
正確做法:
使用專門的定期定額複利計算器,輸入每月投入金額、報酬率、投資年期,立即得到精確結果。
結論:72法則主要適用於「一次性投資」,定期定額請使用專用計算工具。
Q3:為什麼72這個數字這麼神奇?有數學證明嗎?
數學原理完整解析:
第一步:複利公式
當投資翻倍時:
2 = (1 + r)^n
兩邊取自然對數:
ln(2) = n × ln(1 + r)
因此:
n = ln(2) / ln(1 + r)
第二步:泰勒級數近似
當r很小時(例如r=0.08,即8%),可以用泰勒級數展開:
ln(1 + r) ≈ r - r²/2 + r³/3 - r⁴/4 + ...
當r<0.15(即15%)時,高階項很小,可以近似為:
ln(1 + r) ≈ r
第三步:簡化公式
代入上面的近似:
n ≈ ln(2) / r
ln(2) = 0.693147...
如果r以百分比表示(例如8%寫成8而不是0.08):
n ≈ 69.3 / r(%)
這就是69.3法則的由來。
第四步:為什麼改成72?
69.3的因數分解:69.3 ≈ 3² × 7.7(不好整除)
72的因數分解:72 = 2³ × 3² = 8 × 9
72的因數:1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72(共12個)
常見報酬率能整除72的情況:
- 6%:72÷6 = 12(整除)
- 8%:72÷8 = 9(整除)
- 9%:72÷9 = 8(整除)
- 12%:72÷12 = 6(整除)
而69.3幾乎無法被任何常見報酬率整除,心算極為困難。
精確度權衡:
使用72代替69.3,在6%~10%的報酬率範圍內,誤差率不超過1%,但心算便利性大幅提升。這是準確性與實用性的最佳平衡。
結論:72不是隨意選的,而是經過數學驗證與實用性權衡後的最佳選擇。
Q4:72法則可以用來計算股票、ETF、基金嗎?還是只適用於定存?
簡短答案:可以用於所有投資工具,但要注意波動性的影響。
詳細說明:
72法則適用於所有有「預期報酬率」的投資:
- ✅ 定存、債券(固定收益)
- ✅ 股票、ETF(長期年化報酬)
- ✅ 基金(平均報酬率)
- ✅ 房地產(長期增值率)
- ✅ 加密貨幣(高風險高報酬)
關鍵在於如何定義「報酬率」:
定存、債券:
- 報酬率固定(例如年利率2%)
- 72法則非常精確
- 適用性:⭐⭐⭐⭐⭐
股票ETF:
- 使用長期年化報酬率(CAGR)
- 例如:台灣50(0050)過去15年年化約7%
- 報酬率每年波動,但長期平均可預測
- 適用性:⭐⭐⭐⭐☆
主動型基金:
- 使用歷史平均報酬率
- 注意:過去績效不代表未來
- 波動性較ETF更大
- 適用性:⭐⭐⭐☆☆
個股:
- 報酬率波動極大
- 只能用假設報酬率做情境分析
- 例如:「如果台積電能維持15%年化報酬,72÷15=4.8年翻倍」
- 適用性:⭐⭐☆☆☆(主要用於情境假設)
注意事項:
- 波動性影響:
- 72法則假設報酬率穩定
- 股票有漲有跌,實際路徑不是平滑的
-
但長期年化報酬可以平滑短期波動
-
使用歷史數據:
- 計算過去10~15年的CAGR
- 作為未來預期報酬的參考
-
記住:歷史不等於未來
-
保守估算:
- 使用保守的報酬率假設
- 例如:0050歷史年化7%,規劃時可用6%
- 留有安全邊際
實戰範例:
案例:小美投資100萬到0050,想知道何時翻倍
第1步:查詢0050歷史年化報酬
- 過去15年(2009~2024):約7%
第2步:用72法則估算
- 72÷7 ≈ 10.3年翻倍
第3步:保守估算
- 考慮未來可能不如過去,用6%估算
- 72÷6 = 12年翻倍
第4步:設定檢查點
- 每3年檢視一次
- 如果實際報酬低於預期,考慮調整策略
結論:72法則可用於任何投資工具,但對於高波動性資產,應該用長期年化報酬率並保守估算。
Q5:72法則有沒有考慮通膨?我應該怎麼調整?
簡短答案:72法則沒有內建考慮通膨,但你可以用實質報酬率調整。
詳細說明:
名目報酬 vs 實質報酬:
名目報酬率(Nominal Return):
- 表面上看到的報酬率
- 例如:投資年化報酬8%
實質報酬率(Real Return):
- 扣除通膨後的真實購買力成長
- 公式:實質報酬率 ≈ 名目報酬率 - 通膨率
- 例如:8%報酬 - 2%通膨 = 6%實質報酬
用72法則計算實質翻倍時間:
案例1:股票投資
- 名目年化報酬:8%
- 台灣平均通膨:2%
- 實質報酬率:8% - 2% = 6%
- 名目翻倍時間:72÷8 = 9年(帳面金額翻倍)
- 實質翻倍時間:72÷6 = 12年(購買力翻倍)
這意味著:
- 9年後,你的100萬變成200萬(帳面)
- 但12年後,購買力才真正翻倍
- 9~12年之間,帳面雖然翻倍,但購買力還不到2倍
案例2:定存陷阱
- 定存利率:1.5%
- 通膨率:2%
- 實質報酬率:1.5% - 2% = -0.5%(負報酬!)
購買力減半時間:72÷0.5 = 144年?
不對!這是負成長,應該這樣算:
72÷2(通膨率)= 36年購買力減半
雖然帳面金額增加1.5%,但購買力每年實際減少0.5%,36年後購買力只剩一半。
退休規劃的正確做法:
錯誤做法:
- 目標:60歲退休需要2000萬
- 現在35歲,有500萬
- 需要4倍成長(144法則)
- 144÷8% = 18年(53歲達標)
- ❌ 但這沒考慮通膨!
正確做法:
- 第1步:計算實質報酬率
- 投資報酬8% - 通膨2% = 6%實質報酬
- 第2步:調整未來目標金額(考慮通膨)
- 25年後的2000萬,相當於現在的購買力
-
2000萬 × (1.02)²⁵ ≈ 3280萬(未來需要的名目金額)
-
第3步:計算需要的名目報酬率
- 500萬 → 3280萬(6.56倍)
- 需要的報酬率:ln(6.56)/25 ≈ 7.6%
- 或用72法則反推:500萬翻3倍需要114÷8=14.25年,再翻1倍需要72÷8=9年,合計約23年
簡化公式:
實質翻倍時間 = 72 ÷ (名目報酬率 - 通膨率)
例如:
- 名目報酬7%,通膨2%
- 實質翻倍時間 = 72 ÷ (7-2) = 72 ÷ 5 = 14.4年
通膨率的72法則應用:
購買力減半時間 = 72 ÷ 通膨率
例如:
- 通膨率2%:72÷2 = 36年購買力減半
- 通膨率3%:72÷3 = 24年購買力減半
- 通膨率4%:72÷4 = 18年購買力減半
這個公式能幫助你直觀理解通膨的侵蝕威力。
結論:
- 短期投資(<5年):可以忽略通膨
- 長期投資(>10年):必須考慮實質報酬率
- 退休規劃(>20年):務必用實質報酬率計算,否則會嚴重低估所需金額
Q6:聽說巴菲特都用72法則,這是真的嗎?專業投資人會用嗎?
簡短答案:是真的,72法則是投資大師廣泛使用的心算工具。
華倫·巴菲特的72法則應用:
巴菲特在多次演講和訪談中提到72法則,例如:
1. 波克夏年報中的實例
巴菲特在1963年收購波克夏·哈薩威時,股價約$7美元。到2024年,B股價格約$365(A股約$54萬)。
用72法則回推:
- 61年間成長約52倍(7→365)
- 翻倍次數:2⁵=32倍,2⁶=64倍,介於5~6次翻倍
- 平均每次翻倍約10~12年
- 72÷11 ≈ 6.5%複合成長率
這與巴菲特長期年化報酬約19.8%有差距,但72法則能快速粗估數量級。
2. 教育投資人的工具
巴菲特在給股東的信中寫道:
"The most powerful force in the universe is compound interest."
(宇宙中最強大的力量是複利)
他常用72法則向一般投資人解釋:
- 為什麼「穩定的7%報酬」勝過「波動的15%報酬」
- 為什麼長期投資比短線交易更有效
- 為什麼手續費、管理費會大幅侵蝕報酬
其他投資大師的使用:
查理·蒙格(Charlie Munger):
巴菲特的合夥人蒙格也是72法則的愛用者,他強調:
- 「簡單的數學是致富的關鍵」
- 72法則幫助投資人避免複雜的衍生性商品陷阱
- 專注於長期穩定報酬,而非短期高報酬
彼得·林區(Peter Lynch):
富達麥哲倫基金傳奇經理人林區在《彼得林區選股戰略》中提到:
- 用72法則快速評估公司成長性
- 例如:EPS年成長12%,72÷12=6年盈餘翻倍
- 這能幫助判斷股價是否合理
專業投資人如何使用72法則:
1. 機構投資人
- 快速篩選投資標的
- 向客戶說明投資方案
- 董事會簡報時的快速估算
2. 財務顧問
- 與客戶溝通時的視覺化工具
- 解釋複利概念比任何圖表都清楚
- 幫助客戶設定合理預期
3. 基金經理人
- 快速比較不同資產配置
- 評估再平衡策略
- 壓力測試(不同報酬率情境)
為什麼專業人士還用這麼簡單的工具?
原因1:速度
- 會議中即時回應問題
- 不需要打開Excel或計算機
- 3秒內給出合理估算
原因2:溝通
- 客戶聽得懂
- 團隊成員快速對齊
- 避免過度複雜化
原因3:直覺培養
- 建立對數字的敏感度
- 快速識別不合理的假設
- 避免被複雜模型誤導
原因4:謙遜
- 承認預測的不確定性
- 粗略但穩健的估算勝過精確但錯誤的預測
- 保持簡單(Keep It Simple)
知名案例:
巴菲特的複利神話
1956年巴菲特成立合夥基金,初始資金$10萬美元。
- 年化報酬約20%
- 72÷20 = 3.6年翻倍
- 60年間翻倍約16~17次
- 2¹⁶ ≈ 65,000倍
- 理論上:$10萬 × 65,000 = $65億
實際上波克夏市值超過$7000億,證明複利的驚人威力。
結論:
- 72法則不是「新手工具」,而是智慧的簡化
- 巴菲特、蒙格等大師都使用,證明其實用價值
- 簡單不等於膚淺,有時最簡單的工具最有力量
- 專業投資人用72法則做初步判斷,再用精確工具深入分析
Q7:72法則可以用來計算「負報酬」嗎?例如虧損或貶值?
簡短答案:可以,但要注意數學上的調整。
詳細說明:
72法則的原始公式是為正報酬設計的(資產成長),但反向思考,也可以用於負報酬(資產衰減)。
數學調整:
當資產減半時(而非翻倍):
- 原公式:2 = (1 + r)^n
- 減半公式:0.5 = (1 - r)^n
取自然對數:
n = ln(0.5) / ln(1 - r) ≈ ln(0.5) / (-r) = 0.693 / r
因此:
減半年數 = 69.3 ÷ 虧損率(%)
或近似為:
減半年數 ≈ 72 ÷ 虧損率(%)
實際應用案例:
案例1:股票虧損
- 投資100萬在某高風險股票
- 每年平均虧損10%
- 72÷10 = 7.2年資產減半
- 7.2年後只剩約50萬
案例2:匯率貶值
- 某國貨幣每年貶值5%
- 72÷5 = 14.4年購買力減半
案例3:車輛折舊
- 新車每年折舊約15%
- 72÷15 = 4.8年價值減半
- 新車100萬,5年後約剩50萬(符合實際狀況)
案例4:通膨侵蝕(前面提過)
- 通膨率3%
- 72÷3 = 24年購買力減半
注意事項:
1. 精確度問題
負報酬率的72法則誤差比正報酬率稍大,因為:
- ln(1 - r) 的泰勒展開與 ln(1 + r) 不對稱
- 虧損率越大,誤差越明顯
精確度比較:
| 虧損率 | 精確減半時間 | 72法則 | 誤差 |
|---|---|---|---|
| 5% | 13.51年 | 14.4年 | +0.89年 (+6.6%) |
| 10% | 6.58年 | 7.2年 | +0.62年 (+9.4%) |
| 15% | 4.27年 | 4.8年 | +0.53年 (+12.4%) |
| 20% | 3.11年 | 3.6年 | +0.49年 (+15.7%) |
可以看到,虧損率越高,72法則的誤差越大。
2. 建議改用69或70
對於負報酬率,使用69或70會更精確:
| 虧損率 | 精確時間 | 69法則 | 誤差 |
|---|---|---|---|
| 5% | 13.51年 | 13.8年 | +0.29年 (+2.1%) |
| 10% | 6.58年 | 6.9年 | +0.32年 (+4.9%) |
| 15% | 4.27年 | 4.6年 | +0.33年 (+7.7%) |
3. 極端虧損不適用
當虧損率>20%時,72法則誤差超過15%,應該用精確計算。
複合虧損的恐怖:
為什麼虧損比獲利更可怕?
假設你有100萬:
- 情境A:虧損50%,再賺50%
- 100萬 → 50萬(-50%)
- 50萬 → 75萬(+50%)
- 最終虧損25%
- 情境B:賺50%,再虧損50%
- 100萬 → 150萬(+50%)
- 150萬 → 75萬(-50%)
- 最終虧損25%
虧損後需要更高報酬才能回本:
| 虧損幅度 | 需要的報酬率才能回本 | 用72法則估算回本時間(假設年報酬10%) |
|---|---|---|
| -10% | +11.1% | 72÷10 = 7.2年(需要額外11.1%報酬) |
| -20% | +25% | 約需2~3年(72÷10=7.2年,但需25%報酬) |
| -30% | +42.9% | 約需4~5年 |
| -50% | +100% | 72÷10 = 7.2年(需要翻倍) |
| -75% | +300% | 非常困難 |
啟示:
- 避免大幅虧損比追求高報酬更重要
- 虧損50%需要100%報酬才能回本
- 這就是為什麼巴菲特說:「投資第一條:不要虧錢;第二條:記住第一條」
實務應用:
停損策略:
如果設定停損點為-20%:
- 虧損20%後需要25%報酬回本
- 假設年報酬10%,72÷10=7.2年
- 但實際上需要2~3年(因為需要25%額外報酬)
- 評估是否值得等待,還是認賠出場
結論:
- 72法則可以用於負報酬(虧損、貶值、通膨)
- 但精確度較差,建議改用69法則
- 負報酬凸顯了「避免虧損」的重要性
- 理解複合虧損的可怕,比理解複利成長更重要
參考資料
-
Investopedia - Rule of 72: Definition, Usefulness, and How to Use It
網址:https://www.investopedia.com/terms/r/ruleof72.asp
權威財經百科,詳細解釋72法則的數學原理、歷史背景與實務應用案例,包含與69.3法則、70法則的比較分析。 -
The Balance - How to Use the Rule of 72 to Estimate Returns
網址:https://www.thebalancemoney.com/the-rule-of-72-357084
實用的投資理財指南,提供72法則在退休規劃、通膨計算、投資決策中的具體應用範例,並包含常見錯誤與注意事項。 -
美國證券交易委員會(SEC) - Compound Interest Calculator
網址:https://www.investor.gov/financial-tools-calculators/calculators/compound-interest-calculator
美國官方投資者教育平台,提供複利計算工具與72法則的標準解釋,適合驗證72法則的精確度與實際應用。